前回の記事は， MCMC はパラメーターを推定するだけではなく，データの生成にも利用できるというものでした。今回はデータが生成できて何がうれしいのかということを少しだけ真面目に考えてみます。

結論から言えば， MCMC の中にデータ生成を組み込むことで， MCMC が正しく実装されているかの診断ができるようになります。では，どのようにデータ生成が利用できるかを見ていきましょう。

なお，後でコードが出てきますが，一部の関数が定義されていないので動きません。動くサンプルは Gist で入手可能です。

前回のスライドに書いた通り，パラメーターからのサンプリングとデータの生成は，ちょうど入力と出力が逆になっている関係です。数式で表現すると次のようになります。

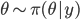
MCMC を経験していると，この並んだ 2 つの式が， Gibbs サンプリングに見えてくるかもしれません。そのように考えると，この 2 つのサンプリングを繰り返すことで，ある分布 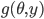が存在して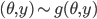， となります。

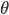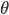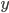ここで興味があるのは の周辺分布です。 は の条件付き確率としてサンプルされたものなので，最初の式を 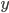について積分してやれば正体がわかります。

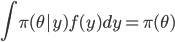
はい，事前分布でした。一生懸命サンプルを集めたと思ったら事前分布だったとは，ただの徒労…と思って諦めてはいけません。もう少し考えてみましょう。

もともと最初の式は 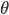の事後分布 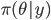からのサンプリングを表したものです。つまり MCMC で普通に作るサンプラーです。一方 2 つ目の式は，統計モデルに従うデータの生成です。おそらく普通は，前者が本当に行いたいことですが，尤度の計算やプログラミングなど，誤りをおかしやすいものです。一方，後者は統計モデルをそのまま自然に記述できるので，比較的容易です。本当に行いたい事後分布からのサンプリングに，簡単なサンプリングを追加すると，周辺分布が出自の知れた事前分布になるということは，非常にうれしいことです。なぜなら，事後分布は一般に解析困難なために，得られたサンプルが正しく事後分布からサンプリングされたものである保証がありません。しかし事前分布は通常よく知られた分布なので，サンプルが事前分布からサンプリングされたものであるかを確認することは，難しくありません。例えば Kolmogorov-Smirnov 検定を用いたり，あるいはもっと簡便に低次元のモーメントを比較するという方法があります。

具体例を示しましょう。観察値 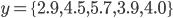が正規分布 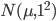から i.i.d. に得られたとき，事前分布を正規分布 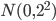として 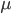の事後分布からのサンプリングを行いたいとします。

このケースでは理論的に 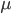の事後分布が簡単に求められるので直接サンプリングしても良いのですが，ここでは簡単に上記のサンプリングが行えることを示すために， Metropolis-Hastings アルゴリズムでのサンプリングを行います。例によって自作乱数フレームワークの FsRandom を使用します。

open FsRandom
open FsRandom.Statistics

[<Literal>]
let pi = System.Math.PI
// 正規分布の対数密度。
let logNormal mu sd x =
   let u = x - mu
   let v = 2.0 * sd * sd
   -u * u / v - 0.5 * log (v * pi)

// 事前分布の平均。
let priorMean = 0.0
// 事前分布の標準偏差。
let priorSd = 2.0

// 事前分布を N(0, 2^2)，提案分布を N(0, 1^2) として MH アルゴリズムを構築。
// 事前分布は分散が小さいほうがデバッグしやすい。
let sampler y =
   // 事前分布の対数密度。
   let logPrior mu = logNormal priorMean priorSd mu
   // 対数尤度。
   let logLikelihood mu = Array.sumBy (logNormal mu 1.0)
   // 提案分布。
   let propose current = normal (current, 1.0)
   let chain = Seq.markovChain (fun (current, y) -> random {
      let! candidate = propose current
      let alpha =
         // 事前分布が対称な分布なので提案分布の比は常に 1 (log スケールで 0) なので省略する。
         let p mu = logLikelihood mu y + logPrior mu
         exp <| p candidate - p current
      let! u = uniform (0.0, 1.0)
      let next = if u <= alpha then candidate else current
#if DEBUG
      let! y = Array.randomCreate 5 (normal (next, 1.0))
#endif
      return (next, y)
   })
   // mu の初期値はなんでもよいのでとりあえず 0 にしておく。
   chain (0.0, y)

// 初期条件
let y = [|2.9; 4.5; 5.7; 3.9; 4.0|]
let state = createState xorshift (123456789u, 362436069u, 521288629u, 88675123u)

let samples =
   sampler y state
   |> Seq.skip 500   // バーンイン
   |> Seq.takeBy 10  // 自己相関を避けるため
   |> Seq.take 1000  // サンプル数
   |> Seq.map fst
   |> Seq.cache
   
printfn "Prior"
printfn "* Mean = %.3f" <| priorMean
printfn "* S.D. = %.3f" <| priorSd
printfn "Sample"
printfn "* Mean = %.3f" <| Seq.average samples
printfn "* S.D. = %.3f" <| sqrt (Seq.var samples)
printfn "Posterior (theory)"
let varTheory = 1.0 / (float (Array.length y) + priorSd ** (-2.0))
let meanTheory = varTheory * Array.sum y + priorMean
printfn "* Mean = %.3f" <| meanTheory
printfn "* S.D. = %.3f" <| sqrt varTheory

ポイントは 35 行目の 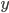のリサンプリングです。 DEBUG シンボルが定義されている場合は 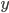がリサンプリングされるために，先述の理由から事後分布は事前分布に一致します。 DEBUG でない場合は真の事後分布からのサンプリングになります。つまり，コンソールへの出力が， DEBUG の有効，無効によって切り替えることができます。

なお，上記のコードは，指定された数おきにシーケンスから要素を取り出す関数 Seq.takeBy とシーケンスの分散を求める Seq.var が定義されていないので，そのままでは動きません。完全版は Gist から入手してください。

まとめ

MCMC のコードは事後分布からのサンプリングを行いたいものですが，事後分布から正しくサンプリングを行えているか保証できません。サンプリング過程で，モデルからのデータ生成を組み入れることで， MCMC は事前分布からのサンプリングになります。事前分布は性質が既知であるため， MCMC が正しく実装できているかの診断に利用できます。

Stan でやってみたかったのですが，サンプリング中にデータの差し替えができない (data ブロックの動的変更ができない) ので，諦めた結果が前回のスライドというオチでした。

参考文献

• Geweke (2004) "Getting it Right: Joint Distribution Tests of Posterior Simulators"
• 大森 (2008) 「マルコフ連鎖の収束判定と効率性の診断」

更新履歴

• [2014-02-28 11:30] 式の修正。
• [2014-03-03 14:30] Gist へのリンクを追加。