データ拡大 (data augmentation) という手法があって，それを MCMC に応用したサンプリング法があります。
分布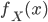 
からの直接サンプリングが困難である場合， 
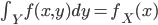となるような 
を構築してやります。ここで 
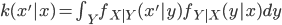を考えると， 
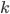は常に非負で 
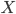について積分すると 1 になるので 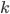がマルコフ連鎖を作るということを利用します[A]。要するに高次元に持っていくことでギブスサンプラーが構築できるよ，ということだと思います。
以下に例を示します。
自由度 4 の t 分布からのサンプリングを行うとします。確率密度関数は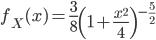 
です。ここで 
(ただし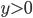 
) を用意してやると， を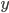 
で積分した結果が 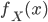になっています[B]。 は 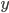を固定すると平均 0，分散 
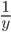の正規分布に比例し， 
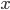を固定すると形状パラメーター 
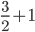，尺度パラメーター 
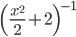のガンマ分布に比例しています。したがってこれらの分布からのサンプリングを繰り返し交互に行うことで，目的の分布からのサンプルを得ることができます。
// データ拡大サンプリング法
let dataAugmentation x y x0 =
state {
let! y' = y x0
let! x' = x y'
return x'
}
// 条件付き確率
let x y = state { return! normal (0.0, sqrt <| 1.0 / y) }
let y x = state { return! gamma (5.0 / 2.0, 1.0 / (x * x / 2.0 + 2.0) }
// サンプリング (自由度 4 の t 分布)
let t4 = dataAugmentation x y
let rec sample (x0, seed) =
seq {
let next = xorshift seed { return! t4 x0 }
yield fst next
yield! sample next
}
乱数をかませているので見た目上は自己相関が低いのですが，実際はアルゴリズムを見れば明らかに直前の状態に依存しています。最初全サンプルで Kolmogorov-Smirnov 検定をして p 値が低くなるので困っていたのですが，数ステップごとのサンプルにしたら綺麗な結果になりました。
例によって自作乱数生成フレームワークを使用しています。実は t 分布からのサンプリングは自作乱数生成フレームワークに定義済みだったりします。
参考文献
- "The data augmentation algorithm: Theory and methodology" in Handbook of Markov Chain Monte Carlo
更新履歴
- [2012-12-13 01:00 更新] が 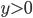であることを追記。