この記事は F# Advent Calendar 2012 のために執筆されました。
昨日の F# Advent Calendar は eozw さんが『F# + ExcelDna + R.NET』という記事を書かれています。 R.NET の中の人としては，感激の至りです[A]。ついでなので宣伝をしておきますと， F# Advent Calendar の裏番組である R Advent Calendar を主催していますので， R に興味がある方は是非ご参加ください。既に定員は埋まっていますが，オーバーラン上等な感じでウェルカムです。
そんなこんなで以下本題に移ります。
はじめに
モンテカルロ法を行う際は様々な乱数を使います。例えば正規分布にしたがう乱数やポアソン分布にしたがう乱数です。基本的には標準乱数 (0 から 1 の間の乱数) が生成できれば他の乱数は生成できるので，究極的には System.Random クラスさえあれば良いのですが，当然そのままでは使いづらいので何らかの解決策が必要になります。
解決策の 1 つは型拡張で所望の乱数を生成するメソッドを追加する方法です。
type System.Random with
// 平均 1/rate の指数分布にしたがう乱数を生成
member this.NextExponential (rate) =
let u = this.NextDouble ()
-log (1.0 - u) / rate
この方法の難点は，別の疑似乱数生成器を使いたくなった場合に Random クラスを継承しなければならないことです。 Sample メソッドの説明を読むと結構面倒くさいことがわかります[B]。それに Sample メソッドはアクセシビリティが protected で F# 的に微妙な感じがしますね[C]。
ということで， F# と相性の良い乱数生成フレームワークが欲しくなってきます。 F# らしいといえば，そう，コンピュテーション式ですね。最近はまってます。そんなわけでコンピュテーション式を利用した F# のための乱数生成フレームワークを作ったのでその紹介をします。
導入
ソースコードは GitHub で，生成物は NuGet で，それぞれ公開しています。好きな方を選んでください。
NuGet でのパッケージ名は RecycleBin.Random ですので，以下のコマンドでインストールできます。
Install-Package RecycleBin.Random
使い方
使う際は，既に述べたように，コンピュテーション式を利用します。以下のような感じで乱数生成できます。
let initialSeed = 123456789u, 362436069u, 521288629u, 88675123u
let randoms, nextSeed =
xorshift initialSeed {
let! u = uniform (-1.0, 1.0) // 一様乱数
let! z = normal (0.0, 1.0) // 正規乱数
return (u, z)
}
printfn "%A" randoms
名前から想像できるように， Xorshift アルゴリズムを利用した乱数生成 (ここでは一様乱数と正規乱数) を行っています。 initialSeed は乱数シードで，乱数生成によって動いた結果の次のシードを nextSeed として返しています。
一様乱数や正規乱数の他にもガンマやポアソンなど様々な乱数生成関数を定義しています。詳しくはソースコードリポジトリ内の README を参照ください。後述のように自分で乱数生成関数を定義するのも容易です。
さて，前述の例では乱数は一度に 1 組だけ生成する形になっています。普通はたくさん乱数を使いたいので，そのような場合には再帰関数を定義します。例えばランダムなバイナリ列を得たい場合にはベルヌーイ分布にしたがう乱数を使って次のような関数を定義します。
let rec binaries initialSeed =
seq {
let binary, nextSeed = xorshift initialSeed { return! bernoulli 0.5 }
yield binary
yield! binaries nextSeed
}
他に getRandomBy という関数を使って乱数の変換を容易に行うことができます。次の 3 つの式は同じ値を返します。
xorshift seed {
return! getRandomBy (fun x -> 2.0 * x) <| uniform (0.0, 1.0)
}
xorshift seed {
let! u = getRandom <| uniform (0.0, 1.0)
return 2.0 * u
}
xorshift seed {
let! u = uniform (0.0, 1.0)
return 2.0 * u
}
拡張
このフレームワークの大きな特徴として乱数生成器と乱数生成関数が分離されているという点が挙げられます。乱数生成器はランダムさを生成するもの，乱数生成関数は乱数生成器が生成したランダムさを利用して別のランダムさを作り出す関数です。最初の例で言うと，xorshift が乱数生成器， uniform と normal が乱数生成関数です。これらが互いに独立していることがポイントです。乱数生成器と乱数生成関数を分離することにより，柔軟に拡張することができます。
以下で乱数生成器と乱数生成関数を独自に定義する方法について見ていきます。
乱数生成器
独自の乱数生成器を定義する方法について説明する前に，乱数生成器がどのように差し替えられるかについて見ていきます。フレームワークに systemrandom という乱数生成器があらかじめ定義されています。名前の通り System.Random クラス (とそれを継承するクラス) を利用します。最初の例を次のように書き換えることができます。
let initialSeed = System.Random ()
let randoms, nextSeed =
systemrandom initialSeed {
let! u = uniform (-1.0, 1.0)
let! z = normal (0.0, 1.0)
return (u, z)
}
全体の流れは全く変わっていないのがわかりますね。乱数生成器の変更は，ごくわずかの修正で済みます。ちなみに systemrandom が返す nextSeed は initialSeed と同じ Random クラスのインスタンスへの参照です。
さて，いよいよ自分で乱数生成器を定義する方法について説明します。乱数生成器を作るために，型が Prng<'s> = 's -> uint32 * 's ('s は乱数シードの型) であるような乱数生成アルゴリズムを実装した関数を用意します。型名の PRNG というのは pseudo-random number generator (疑似乱数生成器) の頭字語です。 uint32 の乱数を返す関数を定義するだけなので， Random クラスを継承するより簡単です[D]。定義した関数を，フレームワーク内に定義された random という関数に放り込んでやれば，乱数生成器の完成です。
例えば線形合同法を実装した乱数生成器を次のように定義できます。
let linearPrng (a, c) x = x, a * x + c // (mod 2^32) let linear (a, c) seed = random (linearPrng (a, c)) seed let myLinear = linear (1664525u, 1013904223u) // Numerical Recipes
random という関数の正体は，ビルダークラスのコンストラクターをカリー化した関数です。これに乱数生成アルゴリズムを実装した関数を部分適用してやることで，乱数シードを与えるとビルダーを返す関数を作成できます。
定義した myLinear を用いて，最初の例が次のように書き換えられます。
let initialSeed = 123456789u
let randoms, nextSeed =
myLinear initialSeed {
let! u = uniform (-1.0, 1.0)
let! z = normal (0.0, 1.0)
return (u, z)
}
先ほど systemrandom でも見た通り，修正はごくわずかで済みます。
フレームワーク内定義されている乱数生成器は， Xorshift アルゴリズム (xorshift) と Random クラスを使うもの (systemrandom) 以外では，科学計算でメジャーな乱数生成器である Mersenne Twister (mersenne) と，その改良である SIMD-Oriented Fast Mersenne Twister (sfmt， ただし SIMD サポートはなし) が実装されています。例で示した線形合同法は簡単に実装できますが，周期が高々 232 と短いので使わない方が良いでしょう。
乱数生成関数
乱数生成関数は uniform や normal のようにフレームワーク内にメジャーなものがいくつか定義されていますが，汎用な関数しか定義されていません。自分が望む形の乱数が欲しい場合は自分で乱数生成関数を定義してやる必要があります。
乱数生成関数の型は PrngState<'s> -> 'a * PrngState<'s> ('s は乱数シードの型， 'a は乱数の型) で， PrngState<'s> = Prng<'s> * 's です。型は複雑ですが，次の例を見る通り実装は難しくありません。標準乱数を 2 つ生成してその積を返す乱数生成関数 g を書いてみましょう。
let g =
state {
let! u1 = ``[0, 1)`` // ``[0, 1)`` は [0, 1) の標準乱数
let! u2 = ``[0, 1)``
return u1 * u2
}
新しく state というコンピュテーション式が出てきましたね。これはいわゆる state モナドというやつです。詳しくは触れませんが，乱数生成器の状態をコンピュテーション式の内部で持ちまわっていますが，乱数生成関数は乱数生成器の状態について関与しません。
ところで，例で標準乱数を生成する関数として ``[0, 1)`` というのを用いています。標準乱数の生成関数はこの他に ``(0, 1)``，``(0, 1]``，``[0, 1]`` があります。このような直観的な名前が利用できるのは便利ですね[E]。もし C# でこれらの関数を定義するとしたら，名前を StandardRandomLowerInclusiveUpperExclusive みたいな冗長な名前を付けて区別するか，もしくは StandardRandom(true, false) のように呼ぶたびに引数を指定してやらなければならないですね。
閑話休題，作成した乱数生成関数は，次のように使うことができます。
let r, _ = xorshift seed { return! g }
独自の乱数生成関数を定義せずとも，実際のところ，次のようにすれば全く同じ乱数を取得することができます。
let r, _ =
xorshift seed {
let! u1 = ``[0, 1)``
let! u2 = ``[0, 1)``
return u1 * u2
}
しかし，この方法では，乱数生成関数が独立していないので，使いまわすことができません。
フレームワークの正体
前節でも少し出てきたのでお分かりかもしれませんが，結局のところ，このフレームワークの正体は state モナドに薄い皮をかぶせただけのものです。ここで state モナドの解説はしません (できません)。参考資料として bleis-tift さんの『モナドハンズオン前座』を推薦します。なごやこわい。
State モナドにおける state の型は， 's -> 'a * 's という関数になっています。状態 's を受け取って，結果 'a と遷移した状態 's を返します。振り返ってみると，乱数生成器の型は 's -> uint32 * 's でまさに state ですし，乱数生成関数もまた PrngState<'s> -> 'a * PrngState<'s> で state ですね。
モナド自体はどうでも良いのですが，モナドを利用することで，重要な性質が容易に実現できます。それは，乱数シードに同じ値を与えてやれば，常に同じ値が返るということです。つまり，乱数シードを保存しておくだけで，任意に結果が復元できます。日本よ，これが純粋関数乱数だ。
ベンチマーク
Random クラスを使うのと比べて速度はどうなの，ということで比べてみました。シーケンス式で 100 万個の [0, 1) の標準乱数を生成してその和を計算するということをやりました。
let rec recyclebin (builder : 's -> RandomBuilder<'s>) seed =
seq {
let u, next = builder seed { return! ``[0, 1)`` }
yield u
yield! recyclebin builder next
}
let rec dotnet (r : Random) =
seq {
let u = r.NextDouble ()
yield u
yield! dotnet r
}
let time action =
let stopwatch = Stopwatch ()
try
stopwatch.Start ()
action ()
finally
stopwatch.Stop ()
printfn "%A" stopwatch.Elapsed
let test generator seed () =
generator seed |> Seq.take 1000000 |> Seq.sum |> ignore
let r = Random ()
let seed = 123456789u, 362436069u, 521288629u, 88675123u
time <| test dotnet r
time <| test (recyclebin xorshift) seed
time <| test (recyclebin systemrandom) r
| 環境 | System.Random |
xorshift |
systemrandom |
|---|---|---|---|
| Windows 7 (.NET 4.5), Intel Core 2 Duo CPU P8600 @ 2.40GHz | 00:00:00.1728638 | 00:00:00.4640198 | 00:00:00.5187938 |
| Ubuntu (Mono 3.0.1), Intel Core 2 Duo CPU T7700 @ 2.40GHz[F] | 00:00:00.6000679 | 00:00:02.2430703 | 00:00:02.2077234 |
他のケースではまた結果が変わってきますが，大体 2.5 倍から 5 倍くらい遅くなっています。絶対時間で言えばそんなに大きなコストではないので，普段使いではそこまで大きな問題にはならない気がします。ガチな計算系で生成する乱数が兆とかのオーダーになってくると，計算時間が日のレベルで変わってくるので，厳しいかもしれません。そこまでくると並列化とか別のアイディアの方が重要になってきますが…[G]。
ちなみにスペースの都合で結果には載せていませんが， Windows 上だと mersenne は xorshift や systemrandom より少し速く， sfmt は少し遅いです[H]。
例題
最後にもう少し具体的な問題を設定してみます。 n 次元単位球の体積をモンテカルロ法で求めてみましょう。単位球を内包するような空間にランダムな点を沢山打って，球内に入った点の割合から体積が推定できます。そこで球に外接する 1 辺の長さが 2 の超立方体にランダムな点を沢山生成します。
let randomPoint n =
state {
let point = Array.zeroCreate n
for index = 0 to n - 1 do
let! u = uniform (-1.0, 1.0)
point.[index] <- u
return point
}
let rec randomPoints n initialSeed =
seq {
let point, nextSeed = xorshift initialSeed { return! randomPoint n }
yield point
yield! randomPoints n nextSeed
}
ランダムに K 個の点を打つと，超立方体の体積が 2n なので，球の内部に入った点の重みを 2n，入らなかった点の重みを 0 にしてやり，その加重平均を求めれば，それが球の体積の推定値になります。計算精度の問題がありますが，それはここでは無視しておきます。
let isInBall n point = Array.sumBy (fun x -> x * x) point <= 1.0 let weight n point = if isInBall n point then pown 2.0 n else 0.0 let estimate n seed K = randomPoints n seed |> Seq.take K |> Seq.averageBy (weight n)
後は適当に乱数シードと繰り返し回数を指定してやると，球の体積が推定できます。繰り返し回数 K を 10,000,000 回として， n を 2 から 20 まで動かして計算してみます。 n 次元単位球の体積は理論的に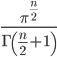 
と求めることができますので，並べて出力してみます。
let sqrtPi = sqrt Math.PI
let volumeBall n =
let halfIntGamma n = // Gamma(n/2 + 1)
if n % 2 = 0
then
Seq.fold (fun acc i -> float i * acc) 1.0 <| seq { 1 .. n / 2 }
else
Seq.fold (fun acc i -> (float i - 0.5) * acc) sqrtPi <| seq { 1 .. (n + 1) / 2 }
sqrtPi ** float n / halfIntGamma n
let K = 10000000
printfn "n,estimate,truth"
[2 .. 20]
|> List.iter (fun n -> printfn "%d,%f,%f" n (estimate n initialSeed K) (volumeBall n))
実際に試しても良いですが，結構時間がかかります。結果だけ欲しい人はこちら (result.csv)。ちょっとだけ試したい人は K を 100,000 くらいに減らして試すと良いでしょう。
実行して誤差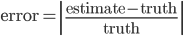 
をグラフにしたのが次の図です。各 n につき 1 回ずつしか測定していません。エラーバーマニアの人ごめんね。
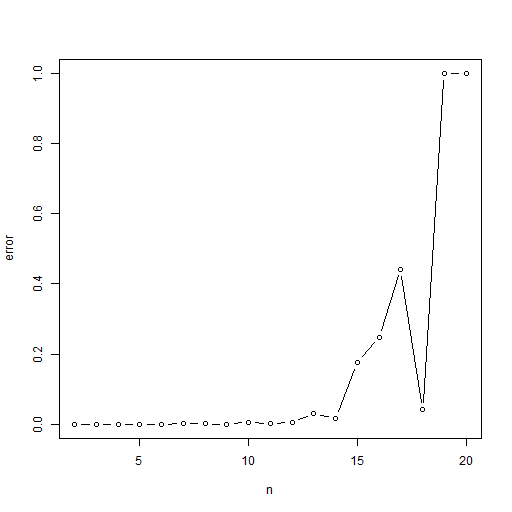
n が小さいときは良く推定できていますが，大きいときでは推定値がかなりずれているのが見てとれます。これは，計算精度の問題も多少はありますが，それ以上に， n 次元球の体積が外接する n 次元立方体に対して小さすぎるため，ランダムに点を打っても球の内部にほとんど点が打たれないということが原因です。この問題は次元の呪いと呼ばれます[I]。例えば n = 20 の場合，球の体積が約 0.026 で，超立方体の体積が 220 なので，その比は 2.5 × 10-8 です。打った点の数が 107 個なので，全然足りていないことがわかります。
話がそれた上に難しい話になりました。現実的な乱数を扱う問題に対しても容易に対応できることが見てとれたと思います。 n 次元球の体積が実用的な問題かどうかは置いといて，一般の乱数を使うケースにおいて十分実用的であると言えるのではないでしょうか[J]。
まとめ
F# のための柔軟な乱数生成フレームワークを作成しました。 Xorshift アルゴリズムや種々の乱数生成関数をあらかじめ定義しているだけでなく，柔軟かつ容易に拡張することもできます。乱数を使う人にとっては，きっと実用的ですよね。
疑問
せっかくの機会なので以下によくわからない点を F# に限らずつらつらと述べます。誰か教えてください。
F# でコンピュテーションを実装する際の型
リリース版の State 型は，本文中にも出てきたとおり 's -> 'a * 's の型略称です (型略称版 StateMonad.fs)。
type State<'s, 'a> = 's -> 'a * 's
一方で次のように判別共用体を使う定義も考えられます。
type State<'s, 'a> = State of ('s -> 'a * 's)
実は別のブランチではこの実装系も一応用意してあります (判別共用体版 StateMonad.fs)。
型略称版が軽量で気軽に利用できる一方で，判別共用体版が頑健で安全に実装できるというイメージです。 F# においてコンピュテーション式を実装する場合に，どういう理由でどちらを選択するべきかといったガイドラインはあるのでしょうか。
For の定義
今の StateBuilder クラスの For メソッドのシグネチャが次のようになっています。
For : seq<'a> * ('a -> State<'s, unit>) -> State<'s, unit>
これを次のようにしたいのです。
For : seq<'a> * ('a -> State<'s, 'b>) -> seq<State<'s, 'b>>
こうできたら yield で seq みたいにもっとスマートに乱数列の生成が書けるのではないかと期待しています。できませんかね。
多変量乱数のテスト
一変量のテストは，連続乱数で Kolmogorov-Smirnov 検定 (KS 検定) と離散乱数で カイ二乗検定 (Χ2 検定) を行っています。多変量の場合の良い方法がわかりません。一応 KS 検定のリンク先に多変量の場合について軽く触れているのですが，いまいち理解できないです…。
一般的な乱数テスト
実はそもそも乱数生成のテストの正しい書き方がわかりません。 KS 検定にしても Χ2 検定にしても，実装が正しくても確率的に失敗することもあれば (偽陽性)，逆に実装が誤っていても成功することもあります (偽陰性)。偽陽性に対してはシードをいじって対応，偽陰性に対してはテスト数を増やす，という感じで良いのでしょうか。
乱数列の並列化
よく見かけるのは乱数シードを変えた複数の乱数生成器を用意するものと，長い周期の乱数列を重複しないような部分列に分割してやるものです。完全な乱数列ならそういう心配は不要なのでしょうが，疑似乱数列ってなんだかよくわからないので相互相関とか怖いのですが，そのあたりについて詳しい文献などはあるでしょうか。
主要参考文献
- 『State Monad in C# and F#』
- 『State モナド』 (『モナドのすべて』より)
- 『モナドハンズオン前座』
F# Advent Calendar 次回予告
明日は nakamura_to さんの『ライブラリを作ってみて感じたF#の良いところや悩みどころ』です。
脚注
- R.NET の更新が止まってるというツッコミは受け付けません。すまぬ…すまぬ…。 [↩]
- 自分で実装する必要はほとんどありません。多くの乱数生成器は Math.NET Numerics で実装されています。 [↩]
- F# で
protectedをオーバーライドすると F# からはprotectedのように扱われて外部からアクセスできませんが， C# からはpublicに見えるので外部から直接呼ばれます。 [↩] uint32を生成するものしかサポートしていないのは今後修正するかもしれません。実はsystemrandomでは 32 ビットの乱数を生成するためにNextBytesを呼んでいるので乱数の無駄遣いをしています。他にも例えば dSFMT のような直接浮動小数点数乱数を生成するような乱数生成器が扱いづらくなっています。 [↩]- もちろん多用は避けるべきでしょうが。 [↩]
- VPS 上の設定。実際の CPU は Xeon らしい。 [↩]
- とはいえもう少し速くなると良いですね。最初は
randomコンピュテーション式を呼ぶたびにRandomBuilderのインスタンスを作っているからだと考えていたのですが，実際に次のような感じにしてみたところ，思ったよりパフォーマンスの改善ができませんでした。しょんぼり。// 1: 補助関数の導入 // 今の RandomBuilder.Run の実装相当 let evaluate prng seed (m : State<PrngState<'s>, 'a>) = m (prng, seed) |> (fun (random, (_, state) : PrngState<'s>) -> random, state) // 使ってみる let u, next = state { return! ``[0, 1)`` } |> evaluate xorshift seed // なにこれ面倒くさい // 2: 上記補助関数を Run に組み込む type RandomBuilder (prng : Prng<'s>) = member this.Run (m) = fun seed -> evaluate prng seed m // 使ってみる let u, next = xorshift { return! ``[0, 1)`` } <| seed[↩]
- SFMT の公式ベンチマーク結果によると SFMT は SIMD サポートがなくても通常の Mersenne Twister より速いらしいのですが，どうしてこうなった。そしてどうして
mersenneがxorshiftより速いの…。 [↩] - 先日ニコニコ生放送の統数研チャンネルで行われた『マルコフ連鎖モンテカルロ法の基礎 第１回』でも言及されていました。 [↩]
- 今回の Advent Calendar のテーマは実用性です。 [↩]