ハミルトニアンモンテカルロ (あるいはハイブリッドモンテカルロ) を F# で実装してみたというお話。ハミルトニアンというのはポテンシャルエネルギーと運動エネルギーの和としてあらわされる物理量のことだそうですが，よくわかりません。わからなくても実装はできるから問題ない(ｷﾘｯ
実用上で重要なのは，確率密度関数の対数をとってマイナスにしたものと，その偏導関数があれば良いということです。確率密度関数の正規化定数は不要です。したがってベイズ推定で事後分布からのサンプリングが必要な場合も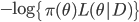 
(
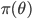は事前分布， 
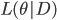は尤度関数) とその偏導関数があれば良いことになります。
open RecycleBin.Random
let inline updateWith f (ys : float []) (xs : float []) =
for index = 0 to Array.length xs - 1 do
xs.[index] <- xs.[index] + f ys.[index]
let inline updateBy f (xs : float []) =
for index = 0 to Array.length xs - 1 do
xs.[index] <- f xs.[index]
let inline cross xs ys = Array.fold2 (fun acc x y -> acc + x * y) 0.0 xs ys
let rec hmc minusLogP gradMinusLogP epsilon step (currentQ, seed) =
xorshift seed {
let d = Array.length currentQ
let q = Array.copy currentQ
let p = Array.zeroCreate d
for index = 0 to d - 1 do
let! z = normal (0.0, 1.0)
p.[index] <- z
let currentP = Array.copy p
updateWith (fun x -> 0.5 * epsilon * x) (gradMinusLogP q) p
for i = 1 to step do
updateWith (fun x -> epsilon * x) p q
if i <> step then updateWith (fun x -> -epsilon * x) (gradMinusLogP q) p
updateWith (fun x -> -0.5 * epsilon * x) (gradMinusLogP q) p
updateBy (fun x -> -x) p
let currentH =
let potential = minusLogP currentQ
let kinetic = cross currentP currentP / 2.0
potential + kinetic
let proposedH =
let potential = minusLogP q
let kinetic = cross p p / 2.0
potential + kinetic
let! r = ``[0, 1)``
if r < exp (currentH - proposedH)
then
return q
else
return currentQ
}
ハミルトニアンモンテカルロ hmc の引数は順に，サンプルしたい密度関数の対数をとってマイナスにしたもの minusLogP，その偏導関数 gradMinusLogP，リープフロッグ積分のステップサイズ epsilon，リープフロッグ積分の長さ step と，現在の状態 currentQ および乱数シード seed です。最初の 2 つは密度関数なので勝手に決まります。最後の 2 つ (1 組) は状態なので，初期値さえ定めれば次以降は後は勝手に決まります。問題はリープフロッグ積分に関わるパラメーターで，複雑なケースではここの調節がなかなか難しいみたいです。
なお，関数中で使用する乱数生成には自作乱数生成フレームワークを使用しています。
例として各変数の分散が 1 で共分散が 0.5 の 2 変量正規分布からのサンプリングを考えます。確率密度関数は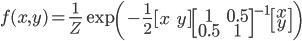 
(
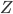は正規化定数) で与えられるので， 
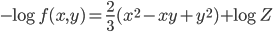です。最初に述べた通り正規化定数は無視して良いので minusLogP はこの関数の最初の項だけ与えてやれば良いことになります。実際に F# でサンプルを得る書いてみると次のようになります。
let minusLogNormal (xs : float []) =
let x, y = xs.[0], xs.[1]
(2.0 / 3.0) * (x * x - x * y + y * y)
let gradMinusLogNormal (xs : float []) =
let x, y = xs.[0], xs.[1]
[|(2.0 / 3.0) * (2.0 * x - y); (2.0 / 3.0) * (-x + 2.0 * y)|]
let h = hmc minusLogNormal gradMinusLogNormal 1.0e-2 1000
let rec sample current = seq {
let next = h current
yield fst next
yield! sample next
}
sample ([|0.0; 0.0|], (123456789u, 362436069u, 521288629u, 88675123u))
|> Seq.take 2000
|> Seq.iter (fun x -> printfn "%f,%f" x.[0] x.[1])
epsilon に 1.0e-2， step に 1000 を与えていますが特に根拠はありません。
ナイーブに実装していますが，例えばハミルトニアンの計算結果を毎回計算しているのを現在の状態として一緒に渡してやるなどすると多少高速化できるかもしれません。