近似ベイズ計算 (approximate Bayesian computation, ABC) は尤度を知らなくても事後分布からのサンプリングが可能な手法です。以前から本ブログでも何度か取り上げており，主な手法を『近似ベイズ計算によるベイズ推定』に挙げています。 ABC はシミュレーションデータと観察データの距離をもとに，シミュレーションデータを生成するパラメーターの採択・棄却を決断するため，非常に時間がかかる方法です。棄却サンプリング法 (ABC-RS) と逐次モンテカルロ法 (ABC-SMC) はパラメーターが高次元になるとサンプリングに時間がかかり， MCMC (ABC-MCMC) の場合は通常の尤度を用いるものに比べてさらに分布の局所ピークに捕らわれやすくなっています。そこで複数の MCMC 連鎖を用いてパラレルテンパリング (parallel tempering; レプリカ交換モンテカルロ法 replica exchange Monte Carlo や Metropolis-coupled MCMC, MC³ とも) を用いる手法にたどり着くのは自然ではないでしょうか。

ということで今回紹介するのは ABC なパラレルテンパリング (ABC-PT) です。

ABC-PT では通常のパラレルテンパリングと同様に，異なるパラメーターを持つ複数の分布からの同時サンプリングを行います。複数の連鎖が頻繁に交換というステップを行うことで，動きの悪い連鎖を他の動きが良い連鎖が救い出すことができます。詳しくは teramonagi 氏の『レプリカ交換モンテカルロ法（パラレル・テンパリング）による混合ガウス分布に従う乱数の生成』を参照ください。

普通 ABC では許容誤差 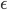を小さく設定すれば良いのですが，これが ABC-MCMC の効率を悪くする最たる原因です。そこで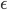， を目的とする小さいものから，動きを活発にするための大きいものまで複数用意し，これらの ABC-MCMC 連鎖間で交換を行い，目的とする事後分布を近似する分布 ( 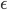が最も小さい連鎖の定常分布) からのサンプリングを行います。

手順

1. 許容誤差 および温度 を適当に設定する。 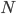は任意に決めた連鎖の数。
2. ABC-RS により からパラメーターを 1 つ採択する。それを とする。同時にパラメーターが生成するデータと観察値との距離 も記録する^[A]。
3. ABC-MCMC ステップ: とする。 について， を確率 で生成する。 は事前に定めた温度 に依存する。 ( は指示関数， は から生成されたシミュレーションデータ) のとき， 確率 で とし (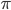 は事前分布)，それ以外の場合は とする。
4. 交換ステップ: すべての連鎖組み合わせから無作為に 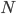ペアを選択する^[B]。選択した連鎖の番号が であるとき， ならば 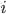番目と 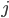番目のパラメーターと距離を交換する^[C]。
5. とし，連鎖が所望の長さに達するまで繰り返す。

が最も誤差が小さいので，これを近似的に事後分布からのサンプルとして利用することができます。

実装

(下図参照) からのサンプリングを行います。原著と同じ例題です。 の周りで密度曲線がわずかに盛り上がっています。

サンプリングしたい分布の確率密度曲線。図を作成する際に [-10, 10] でカットしていないので密度の値は正確ではありませんが，大した違いではないので気にしないでください。

F# で実装します。全コードは ideone.com にアップロードしています。本文では一部の関数について説明を省略します。名前からお察しください。 ideone.com のソースコードには多少コメントを入れてありますのでそちらを参照するとわかりやすいかもしれません。

最初に事前分布からのパラメーターをサンプルする関数を作成します。

let samplePrior (random : Random) = random.NextUniform -10.0 10.0

次に事前分布から得たパラメーターをもとにシミュレーションデータを生成する関数です。

let simulateValue (random : Random) theta =
   let r = random.NextDouble ()
   if r < 0.45
   then
      random.NextNormal theta 1.0
   elif r < 0.90
   then
      random.NextNormal theta 0.01
   else
      random.NextNormal (theta - 5.0) 1.0

ここではシミュレーションデータを 1 つだけ生成します。そのシミュレーションデータの要約統計量と原点の要約統計量の距離が 0 に近ければば良いので，シミュレーションデータそのものを要約統計量とし，距離をその絶対値にします。

let distance x = abs x

いよいよ本丸に突入します。まず最初に棄却サンプリングを行って初期化します。

type AbcResult =
   | Accept of float (* parameter *) * float (* distance *)
   | Reject

let rejection random tolerance theta =
   let x = simulateValue random theta
   let d = distance x
   if d < tolerance
   then
      Accept (theta, d)
   else
      Reject

let rec rejectionInfinite random tolerance =
   seq {
      yield rejection random tolerance (samplePrior random)
      yield! rejectionInfinite random tolerance
   }

let currentLength = ref 0
let current =
   let chooseAcceptance = Seq.choose (function | Accept (theta, d) -> Some (theta, d) | Reject -> None)
   Array.map (rejectionInfinite random >> chooseAcceptance >> Seq.head) tolerance
incr currentLength

頻繁に交換を行うので配列にしておくのが無難でしょう。

以降は ABC-MCMC と交換を繰り返すだけです。

let q (theta, temperature) = random.NextNormal theta (0.10 * 0.10 * temperature)
let isInPriorRange x = -10.0 <= x && x < 10.0

while !currentLength < chainLength do
   // ABC-MCMC ステップ
   let theta = Array.zip (Array.map fst current) temperature |> Array.map q
   let values = Array.map (simulateValue random) theta
   // alpha = min { 1, (π(candidate) * q(current -> candidate)) / (π(current) * q(candidate -> current)) } * 1_ρ(values)
   // q は平均 0 の正規分布なので比は常に 1 になる。
   // π は一様分布なので範囲外で 0，範囲内で 1 で current は常に範囲内にあることが保障される。
   // したがって
   // * candidate が一様分布の範囲内の時 alpha = 1_ρ(values)
   // * candidate が一様分布の範囲外の時 alpha = 0
   for index = 0 to n - 1 do
      let t = theta.[index]
      let x = values.[index]
      let e = tolerance.[index]
      let d = distance x
      if isInPriorRange t && d < e
      then
         current.[index] <- (t, d)

   // 交換ステップ
   for loop = 1 to n do
      let index = sampleWithReplacement random 2 chainIndexes
      Array.sortInPlace index
      let i = Array.min index
      let j = Array.max index
      if i <> j
      then
         let (_, d) = current.[j]
         let e = tolerance.[i]
         if d < e
         then
            swapInPlace i j current

   // その他の処理。現在の状態を出力するなど。
   incr currentLength

以下に結果を示します。

混合分布からのサンプリング (ε₁ = 0.025)。連鎖の長さは 600,000 で最初の 150,000 をバーンインとして捨てた。サンプルは 100 ステップごと (4,500 サンプル)。緑の線は真の分布の確率密度曲線。

うまく の周りもサンプルできていることがわかります。

まとめ

ABC-PT を使うと ABC-MCMC で大きな問題となる局所ピークを上手く回避してサンプリングすることができます。また， MCMC を用いているので従来の ABC-RS のような高次元における非効率を回避することもできます。そして ABC である最大の利点である，複雑な尤度計算が不要で，単にモデルからデータがシミュレーションできるだけで事後分布からのサンプリングを行うことができます。素敵ですね。

参考文献

• Baragatti et al. (2012) Likelihood-Free Parallel Tempering (arXiv v3)

脚注

1. 原著ではデータセットを記録することになっていますが，距離を記録すれば十分だと思います。データセットを記録すると毎回要約統計量と距離を計算することになるので，計算時間の短縮にもなります。 [↩]
2. どうして連鎖数なのかよく理解できません。任意の数で良い気がします。また，復元抽出である意味もわかりません。 [↩]
3. より交換が行われるようにするには，許容誤差の近い連鎖をリングという単位に分割し，リング内でのランダムな交換を行うと良いみたいです。 [↩]