近似ベイズ計算 (approximate Bayesian computation, ABC) と呼ばれるベイズ的手法があります。近似ベイズ計算の「近似」たるゆえんは,複雑な尤度の計算を行わないために,近似計算を行うという点にあります。
そもそも,ベイズの定理は,事後分布 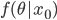 は事前分布
は事前分布 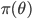 と尤度
と尤度 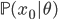 の間に
の間に 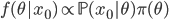 の関係が成り立つことを主張しています。尤度が一般に計算困難であることを考えると,事後分布を求めることはほとんどできなくなってしまいます。 ABC では,
の関係が成り立つことを主張しています。尤度が一般に計算困難であることを考えると,事後分布を求めることはほとんどできなくなってしまいます。 ABC では, 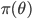 からデータ
からデータ 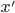 をシミュレーションし,データ間の距離
をシミュレーションし,データ間の距離 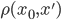 が
が 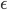 以下であれば許容することにしています。つまり,
以下であれば許容することにしています。つまり, 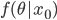 の代わりに
の代わりに 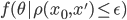 からサンプリングを行えれば良いという考えです。なお,データ間の距離そのものを考えることは難しい場合は,統計量
からサンプリングを行えれば良いという考えです。なお,データ間の距離そのものを考えることは難しい場合は,統計量 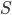 を用いて
を用いて 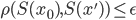 とする場合もあります。
とする場合もあります。
一般に ABC で用いられているフレームワークは次の 3 つです。
- 棄却サンプリング
- マルコフ連鎖モンテカルロ (MCMC)
- 逐次モンテカルロ (SMC)
棄却サンプリング
Tavaré et al. (1997) や Pritchard et al. (1999) で使われた手法で上で述べた方法を単純に実装したものです。アルゴリズムは以下のようになります。
- 候補
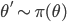 を生成する。
を生成する。 - モデル
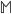 からデータセット
からデータセット 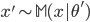 を生成する。
を生成する。 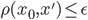 ならば
ならば 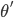 を記録する。
を記録する。- 十分な数を得られるまで繰り返す。
MCMC
棄却サンプリングは小さな 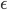 に対して効率が悪いため, Marjoram et al. (2003) は MCMC を使う手法を提案しています。
に対して効率が悪いため, Marjoram et al. (2003) は MCMC を使う手法を提案しています。
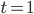 とし,
とし, 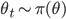 をサンプルする。
をサンプルする。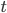 が十分大きくなるまで以下を繰り返す。
が十分大きくなるまで以下を繰り返す。
- 推移核
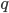 にしたがって
にしたがって 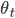 から候補
から候補 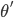 を得る。
を得る。 - モデル
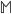 からデータセット
からデータセット 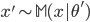 を生成する。
を生成する。 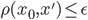 ならば確率
ならば確率 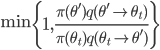 により
により 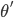 を記録する。記録された場合は
を記録する。記録された場合は 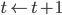 ,
, 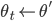 とする。
とする。
- 推移核
推移核は正規分布や t 分布といった対称のものにすれば計算が容易になります。
SMC
Sisson et al. (2007) では SMC を用いたサンプリングが提案されています。 SMC は棄却サンプリングとほとんど一緒ですが,サンプリングを 1 回行うのではなく,許容限界 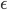 を徐々に小さくしていくことで効率的なサンプリングが行えるようにしています。
を徐々に小さくしていくことで効率的なサンプリングが行えるようにしています。
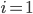 とする。
とする。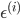 が定義されている間,以下を繰り返す。
が定義されている間,以下を繰り返す。
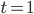 とする。
とする。-
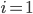 のとき
のとき
- 適当な分布
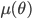 から候補
から候補 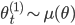 を生成する。
を生成する。 - モデル
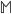 からデータセット
からデータセット 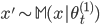 を生成する。
を生成する。 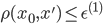 ならば
ならば 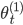 を記録する。記録されたサンプルの重みを
を記録する。記録されたサンプルの重みを 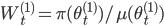 とする。
とする。 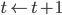 とする。
とする。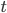 が十分な数 (
が十分な数 (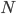 ) になるまで繰り返す。
) になるまで繰り返す。
- 適当な分布
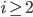 のとき
のとき
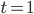 とする。
とする。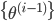 から
から 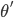 を重み
を重み 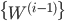 にしたがってサンプルする。
にしたがってサンプルする。- 推移核
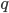 にしたがって
にしたがって 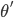 から候補
から候補 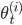 を得る。
を得る。 - モデル
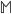 からデータセット
からデータセット 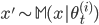 を生成する。
を生成する。 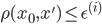 ならば
ならば 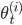 を記録する。記録されたサンプルの重みを
を記録する。記録されたサンプルの重みを 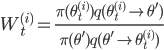 とする。
とする。 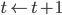 とする。
とする。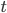 が十分な数 (
が十分な数 (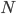 ) になるまで繰り返す。
) になるまで繰り返す。
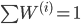 となるように
となるように 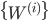 を正規化する。
を正規化する。- もし有効サンプル数
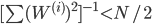 ならば,重み
ならば,重み 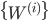 にしたがって
にしたがって 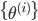 から重複を許したリサンプリングを行い,すべてのサンプル重みを
から重複を許したリサンプリングを行い,すべてのサンプル重みを 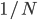 とする。
とする。 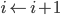 とする。
とする。
- 最後の
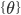 から重み
から重み 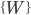 でサンプルする。
でサンプルする。
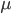 は任意に設定できる分布なので,
は任意に設定できる分布なので, 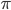 と同じにすれば計算が容易です。推移核も対称のものにすれば計算が容易になります。
と同じにすれば計算が容易です。推移核も対称のものにすれば計算が容易になります。
有効サンプル数が 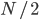 より小さいかどうかの反低位における
より小さいかどうかの反低位における 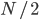 は一般的な値であって,必ずこの値にしなければならないという訳ではありません。
は一般的な値であって,必ずこの値にしなければならないという訳ではありません。
注意点
棄却サンプリングと SMC についてはサンプル数に関して並列化が可能ですが, MCMC ではサンプルが直前のサンプルに依存するために並列化は不可能です。 MCMC では代わりにチェーン数を増やすことで対応することが可能です。しかし,自己相関なども含めて考えれば, SMC が良いのではないかと思います。ただし, MCMC と SMC の方法では推移核をあまり小さくとると偏ったサンプルになることに注意が必要です。棄却サンプリングはその点で調整が不要な点が楽と言えば楽です。また,いずれの場合も事前分布の影響には気をつけた方が良いかもしれません。
追記
- [2011-06-02 22:40+0900 追記] 『近似ベイズ計算の実装例』で ABC-SMC を R で実装しています。
- [2011-06-14 13:50+0900 追記] 本稿で説明しているような分布の形が少しずつ変わっていくタイプの SMC は,ポピュレーション型のモンテカルロ法 (population Monte Carlo) と呼ぶそうです (伊庭 2005; Beaumont et al. 2009)。
