少し前の事ですが ,京都大学で行われた日本遺伝学会第 83 回大会に参加しました。その中の "Kernel Bayesian Computation" という講演が気になりました。
集団遺伝学の世界ではモデルが複雑な場合に尤度を回避できる approximate Bayesian computation (ABC) という手法がよく用いられます。 ABC については本ブログでも『近似ベイズ計算によるベイズ推定』や『Tokyo.R#17』[A] でまとめています。しかし ABC は計算コストが非常に高いのが難点です。
Kernel Bayesian computation (KBC) は ABC と同様に尤度計算を行わずにベイズ推定をする手法なのですが, ABC のような無駄な計算がないのが特徴です。そこで, KBC を R で実装してみました。
[warning]
警告
私自身,まだきちんとカーネル法について理解していないため,本文には誤りを含むかもしれません。誤りに気づかれたらご指摘いただけると幸いです。
[/warning]
手法
比較のために,まず ABC の棄却サンプリング法を述べ,次に KBC の手法を述べます。
ABC
事前準備
- 観察データ
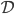 の要約統計量
の要約統計量 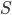 を算出する。
を算出する。 - パラメーターの事前分布
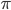 を任意に定める。
を任意に定める。 - 統計値間の距離
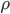 および許容限界
および許容限界 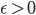 を任意に定める。
を任意に定める。
手順
- パラメーター
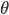 を事前分布
を事前分布 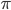 から生成する。
から生成する。 - パラメーター
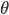 にしたがいシミュレーションデータ
にしたがいシミュレーションデータ 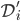 を生成し,その要約統計量
を生成し,その要約統計量 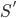 を算出する。
を算出する。 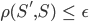 ならば
ならば 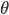 を受容,そうでなければ棄却。
を受容,そうでなければ棄却。- 受容したサンプルが十分な数になるまで繰り返す。
結果
上記の手順で得られたサンプル集合 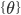 は,事後分布からのランダムサンプルになります。
は,事後分布からのランダムサンプルになります。
KBC
事前準備
- 観察データ
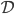 の要約統計量
の要約統計量 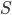 を算出する。
を算出する。 - パラメーターの事前分布
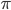 を任意に定める。
を任意に定める。 - パラメーター空間上の特性的な正定値カーネル
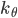 および統計量空間上の正定値カーネル
および統計量空間上の正定値カーネル 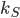 を任意に定める。
を任意に定める。 - 重み
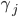
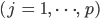 で点
で点 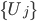 を,事前分布をまんべんなく埋めるようにサンプルする。
を,事前分布をまんべんなく埋めるようにサンプルする。 - 正規化定数
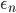 および
および 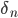 を任意に定める。
を任意に定める。
手順
- パラメーター
 を事前分布
を事前分布 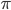 から生成する。
から生成する。 - パラメーター
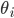
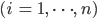 にしたがいシミュレーションデータ
にしたがいシミュレーションデータ 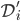 を生成し,その要約統計量
を生成し,その要約統計量 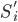 を算出する。
を算出する。 - グラム行列
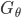 および
および 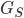 を算出する。
を算出する。 - 特徴空間上の平均の推定量
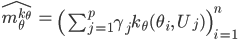 を算出する。
を算出する。 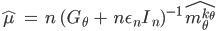 を算出し,
を算出し, 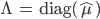 とする。
とする。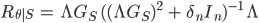 を算出する。
を算出する。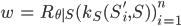 を算出する。
を算出する。
結果
上記で得られた 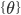 は,事後分布からの重み
は,事後分布からの重み 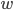 での重み付きサンプルになります。
での重み付きサンプルになります。
R による実装例
例題
KBC の実装にあたり,次の例題を設定します。
- 正規分布
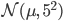 にしたがう 3 点
にしたがう 3 点 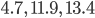 を得た。
を得た。 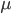 の事後分布を推定したい。
の事後分布を推定したい。 - 事前分布は
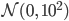 とする。
とする。
なお,この例題は解析的に解く事ができて,事後分布は 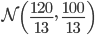 になります。
になります。
実装
まず例題の条件をそのままコードに落とし込みます。
D <- c(4.7, 11.9, 13.4) rprior <- function(n) rnorm(n, 0, 10) rmodel <- function(mu) sapply(mu, function(m) rnorm(3, m, 5))
KBC ではサンプル数は事前に設定します。ここでは 100 とします。また,統計量は平均とします。
n <- 100 S <- mean(D) theta <- rprior(n) S_prime <- colMeans(rmodel(theta))
カーネル関数はガウスカーネルとします。ガウスカーネル関数のパラメーターは適当に選んで良いのですが,ペアワイズ距離の中央値にすると良いそうです[B]。
getKernel <- function(values) {
sigma <- median(dist(values))
function(x, y) as.numeric(exp(-crossprod(x - y) / (2 * sigma * sigma)))
}
k_theta <- getKernel(theta)
k_S <- getKernel(S_prime)
getKernel ではカーネル関数を返します。最後に as.numeric をしないと結果が 1 行 1 列の行列となり扱いにくいので,ベクトルに変換しています。
次にグラム行列を求めます。
gramian <- function(x, kernel) {
if (is.vector(x)) {
x <- matrix(unlist(x), ncol=length(x))
}
n <- ncol(x)
gram <- diag(1, n)
ks <- sapply(seq(n), function(i) kernel(x[, i], x[, i]))
for (i in seq(n)[-1]) {
for (j in seq(i)) {
e <- kernel(x[, i], x[, j]) / sqrt(ks[i] * ks[j])
gram[i, j] <- gram[j, i] <- e
}
}
gram
}
G_theta <- gramian(theta, k_theta)
G_S <- gramian(S_prime, k_S)
特徴空間における平均を計算します。事前分布からランダムに 500 点サンプルして重みを等しく設定します。
p <- 500 U <- rprior(p) gamma <- rep(1/p, p) m_hat <- sapply(seq(n), function(i) sum(sapply(seq(p), function(j) gamma[j] * k_theta(theta[i], U[j]))))
残りの計算をします。ここでは原著に倣い正則化定数を 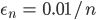 および
および 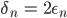 としました[C]。
としました[C]。
epsilon <- 0.01 / n delta <- 2 * epsilon mu_hat <- n * solve(G_theta + n * diag(epsilon, n)) %*% m_hat Lambda <- diag(as.numeric(mu_hat)) LG <- Lambda %*% G_S R <- LG %*% solve(LG^2 + diag(delta, n)) %*% Lambda w <- R %*% sapply(S_prime, function(s) k_S(s, S))
以上で KBC の計算は完了のはずですが,計算精度の問題からなのか,たまに w の中に負の値が出てきます。正しいかどうかはわかりませんが,負の値は 0 にしてしまい,ついでに重みを合計が 1 になるように正規化します。
w <- ifelse(w < 0, 0, w) w <- w / sum(w)
結果
事後平均は weighted.mean 関数を,事後分布の密度推定は density 関数を使います。
posteriorMean <- weighted.mean(theta, w) posteriorDensity <- density(theta, weights=w)
実行例をプロットした結果は次の通りです。比較のために ABC の結果も描いています。この例では ABC も KBC も似たような結果になっています。ついでに言えば,どちらもそんなに良い結果ではないようです。図が誤っていたので差し替えました。事後分布の推定密度曲線をいずれも xlim と ylim を指定していませんでした。また, KBC のカーネルのパラメーターを上の実装とは少し変えてあてはめを良くしています。
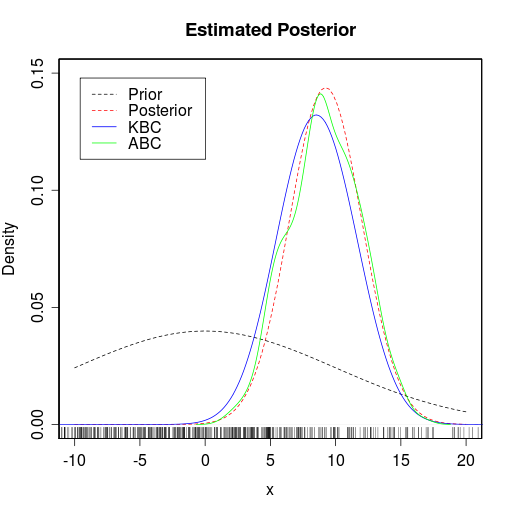
KBC と ABC による事後分布推定。黒と赤の破線はそれぞれ事前分布および真の事後分布を示し,青と緑の実線はそれぞれ KBC と ABC により推定された事後分布を示す。 KBC, ABC のいずれもサンプル数は 200 とし, KBC におけるガウシアンカーネルのパラメーターはパラメーターのカーネルをペアワイズ距離の中央値,統計量のカーネルを 0.1, ABC における許容限界距離は 0.01 とした。
まとめ
最初にも述べた通り, KBC は ABC と比べて無駄な計算がありません。そのため計算時間も圧倒的に速いです。少し実装が複雑になりますが,実行時間を考えれば安いものだと思います。
[2012-09-23 21:20] RPubs に別の混合分布の例を載せました。
参考文献
履歴
- [2011-12-29 05:00] 図の差し替え。
- [2011-12-29 14:15] 図のキャプションに追記。
