6 は完全数です。つまり自身を除いた約数 (1, 2, 3) の総和が自身 (6) になります。 6 の何らかの分割の総和が自身に戻るという例を別にあげてみます。
1 から 6 までの整数 (1, 2, 3, 4, 5, 6) を重複しないように 3 つずつの 2 組に分けます。例えば {3, 1, 6} と {4, 5, 2} のように。好きな方の組を選び,それの要素を 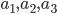 とします。他方の組に
とします。他方の組に 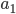 以下の数が
以下の数が 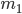 個,
個, 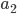 以下の数が
以下の数が 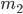 個,
個, 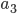 以下の数が
以下の数が 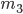 個含まれているとすると,最初の組の分け方,選び方にかかわらず次の数は 6 になります。
個含まれているとすると,最初の組の分け方,選び方にかかわらず次の数は 6 になります。
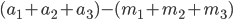
先ほどあげた例では {3, 1, 6} を選べば 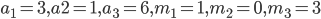 ですので確かに (3 + 1 + 6) - (1 + 0 + 3) = 6 になります。 {4, 5, 2} の方を選んでも同じように上の式の値は 6 になります。
ですので確かに (3 + 1 + 6) - (1 + 0 + 3) = 6 になります。 {4, 5, 2} の方を選んでも同じように上の式の値は 6 になります。
いわゆる数学マジックというやつです。タネを明かすとそんなに難しくないのですが。
当たり前ですが 1 から 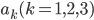 までの数は全部で
までの数は全部で 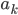 個あります。その
個あります。その 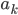 個の内
個の内 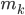 個が選ばれなかった方の組に含まれています。選ばれた方の組には
個が選ばれなかった方の組に含まれています。選ばれた方の組には 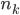 個含まれていたとしましょう。 2 つの組の要素は重複していないので次の関係が成り立ちます。
個含まれていたとしましょう。 2 つの組の要素は重複していないので次の関係が成り立ちます。
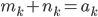
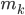 を右辺に移項して書き換えます。
を右辺に移項して書き換えます。
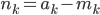
最初の式は 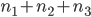 を求めることと同じであることがわかります。つまり
を求めることと同じであることがわかります。つまり 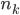 とは何なのかが分かれば良いことになります。
とは何なのかが分かれば良いことになります。
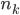 は選んだ組に含まれる
は選んだ組に含まれる 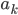 以下の数の個数です。言い換えれば,選んだ組には
以下の数の個数です。言い換えれば,選んだ組には 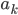 以下の数が
以下の数が 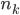 個含まれます。
個含まれます。 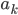 以下という言葉に
以下という言葉に 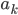 自身を含んでいるので,結局
自身を含んでいるので,結局 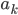 は選んだ組で
は選んだ組で 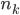 番目に小さい数であるということです。
番目に小さい数であるということです。
さて,選んだ組には 3 つの数が含まれています。その内 1 番目に小さい数, 2 番目に小さい数, 3 番目に小さい数はそれぞれいくつずつ含まれているでしょうか。 3 つの数が重複していないので,当然すべて 1 つずつです。ということは 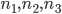 は 1, 2, 3 の組み合わせということになります。どんな順番であるかに関わらず,結局
は 1, 2, 3 の組み合わせということになります。どんな順番であるかに関わらず,結局 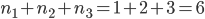 になります。
になります。
以上タネ明かしでした。長く書きましたが至極当たり前のことを難しく言っているだけですね。数学の手品なんて大抵そんなものです。
