Stan で Lasso - 捨てられたブログ

パラメーターが沢山あって困るのでパラメーターを減らしたいという場合があります。ところで lasso です。 lasso はおなじみの L1 ノルムでペナルティーをかけるやつです。その lasso には変数選択としての用法があるとのことです。つまり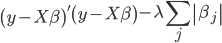を最小にするような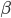を求めてやると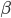，がスパースなので 0 になるような係数はいらないと判断できるわけですね。

というわけでこれを Stan でやってみたいということです。

まず適当にデータを作ります。 20 パラメーターを用意して，実際には 1, 2, 5 番目のパラメーターのみ効いているというデータです。

P <- 20L
N <- 40L

x <- matrix(rnorm(N * P), nrow=N, ncol=P)
y <- 1.5 + as.numeric(x %*% c(3, -2, 0, 0, 1, rep(0, P - 5L)) + rnorm(N, 0, 0.2))

そして Stan モデルを用意してやります。 Stan マニュアルの『50.2. Penalized Maximum Likelihood Estimation』あたりを参考にしながら。

data {
   int<lower=1> N;
   int<lower=1> P;
   matrix[N, P] x;
   vector[N] y;
}
transformed data {
   real<lower=0> lambda;
   lambda <- 0.2;
}
parameters {
   real mu;
   vector[P] beta;
   real<lower=0> sigma2;
}
model {
   real sigma;

   sigma2 ~ inv_gamma(0.001, 0.001);
   sigma <- sqrt(sigma2);

   beta ~ double_exponential(0, sigma / lambda);
   mu ~ normal(0, 50);
   y ~ normal(mu + x * beta, sigma);

   // lasso penalty
   for (i in 1:P) {
      increment_log_prob(-lambda * fabs(beta[i]));
   }
}

λ = 0.2 に特に意味はありません。結果は以下の通り。 20 個ある β のうち最初の 5 つと μ のみプロットしています。

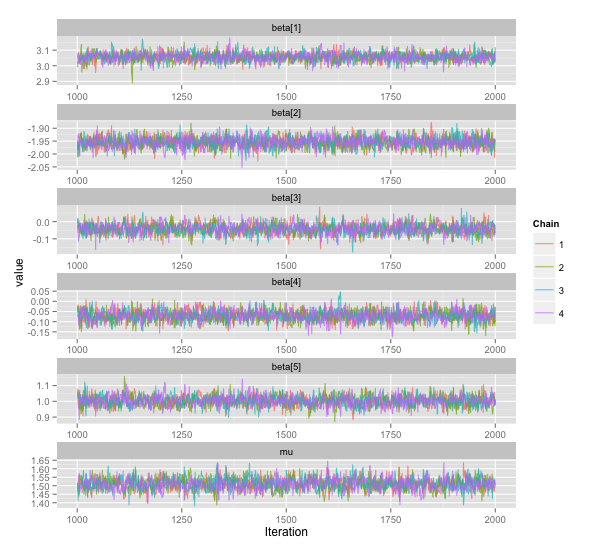
lasso_0-traceplot

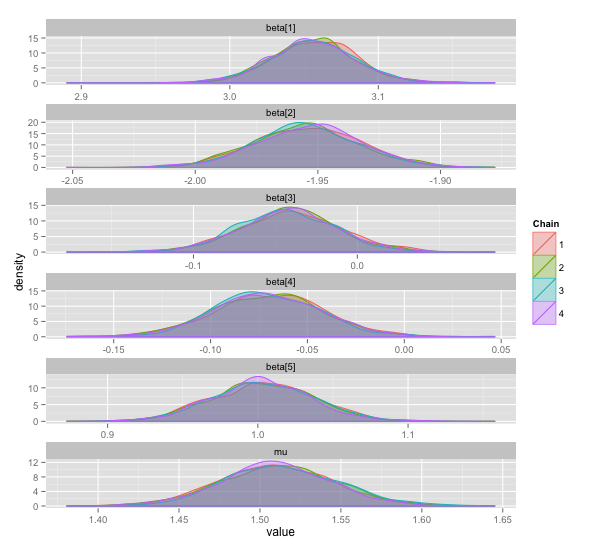
lasso_0-density

まあまあ良いところに落ち着いている気もしますが，もっと 3, 4 番目の β が 0 に寄ってくれると嬉しいですね。適当に λ = 0.2 と決めたのが良くないのかもしれません。この λ というパラメーターはなんかよくわからない。おそらくここを適当に決めてしまうことは，事前分布を適当に決めてしまうよりシビアに効いてくるのでしょう。ということでそのシビアさを少しでも緩和したいので， λ も一緒にサンプリングしたくなります。

// transformed data を消して以下を加えて後は一緒
parameters {
   real<lower=0> lambda;
}
model {
   lambda ~ gamma(0.001, 1);
}

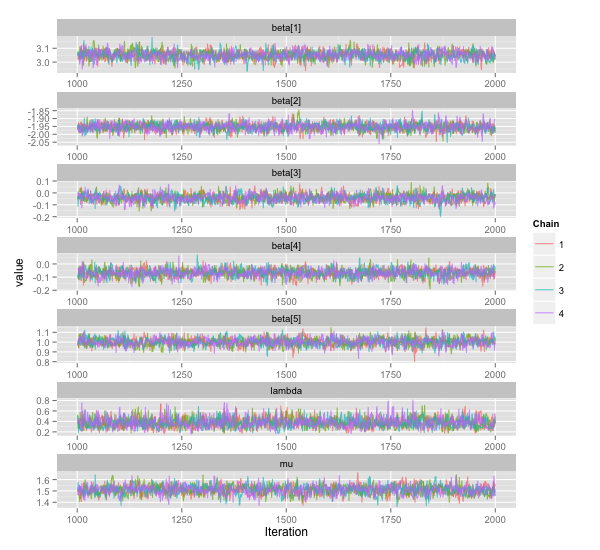
lasso_1-traceplot

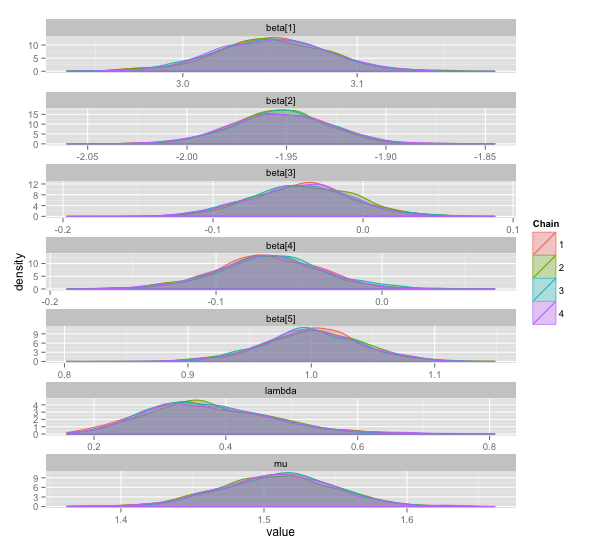
lasso_1-density

良くなった気がします。最初に適当に決めた λ とは，ややずれた値が得られています。

更に階層化してやる方法も参考文献に記載されていますが，とりあえずこんなところで。

ちなみに参考文献で紹介されていた monomvn という R のパッケージを使うと以下のような感じになります。

library(monomvn)

fit <- blasso(x, y, T=10000, thin=2)
beta.estimate <- fit$beta

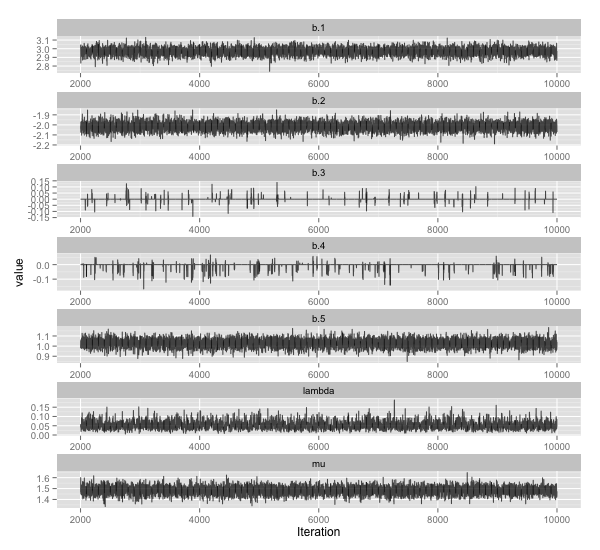
lasso_monomvn-traceplot

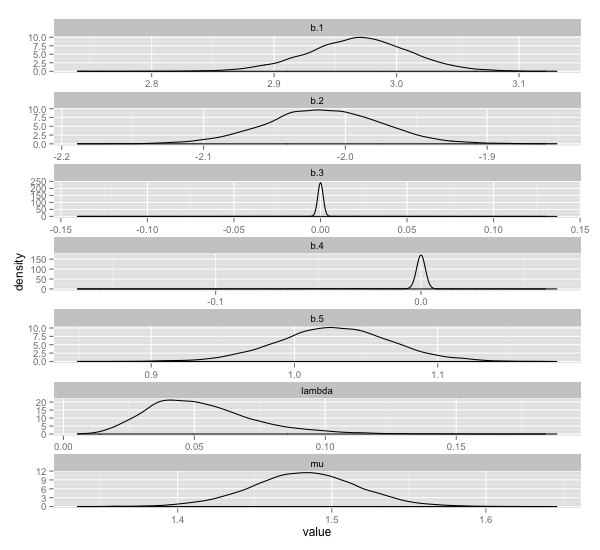
lasso_monomvn-density

こちらのパッケージは Stan でやるのと異なり， (デフォルトで) reversible jump MCMC を用いているため，使用されないパラメーターがある場合はその値が 0 になります。 0 にきれいにピークが出ているのはそのためです。

λ が Stan のものと結構ずれていますね。よくわかりません。