F# でオンライン変化点検知

12 5月, 2014

ChangeFinder と呼ばれるオンライン変化点検知のアルゴリズムがあります。このアルゴリズムはオンラインアルゴリズムです。新しく与えられるデータが，それまでに得られたパラメーターによる時系列モデルからどの程度逸脱してるかというスコアを平滑化して，そのスコアを新たな時系列とした別の時系列モデルに対して同様にスコアを算出します。時系列モデルには自己回帰モデル (AR モデル) のオンラインパラメーター更新版である sequential discounting AR learning (SDAR 学習) と呼ばれる学習モデルが利用される模様です。

簡単な 1 次元時系列データに対する， SDAR 学習による ChangeFinder アルゴリズムを実装してみました。

時系列データ

まずは時系列データを保持するクラスを作成します。 SDAR 学習では AR モデルに使われるための数世代分のデータを保持しておけば良いので，データを追加する度に古いデータを失っていくような実装にします。初期状態ではデータが存在しないので None にしたいところですが，面倒なので NaN を None の代わりにします。

type Series (n) =
   let mutable index = 0
   let buffer = Array.create n nan

   member __.Append (x) =
      index <- (index + 1) % n
      buffer.[index] <- x

   member __.GetBack (back) =
      if back < 0 || n <= back then
         raise <| System.ArgumentOutOfRangeException ("back")
      else
         buffer.[(n + index - back) % n]

さらに平均と分散を求められるようにしておきます。 NaN や無限大を無視するようにしておくことで，データが得られなかった場合でも停止しないようにします[A]。これらの値はスコアの平滑化と AR モデルの初期パラメーターとして利用します。オンラインで更新されていくものなので，演算精度や推定値の不偏性なんかは気にしなくても良いです。

let getData () = Array.filter isFinite buffer

member this.Mean
   with get () =
      match getData () with
         | [||] -> nan
         | array -> Array.average array

member this.Var
   with get () =
      match getData () with
         | [||]
         | [|_|] -> nan
         | array -> Array.averageBy (fun x -> x * x) array - pown (Array.average array) 2

ここで使われる isFinite は NaN でも無限大でもないということ調べる関数です。

let inline isNaN x = (^a : (static member IsNaN : ^a -> bool) x)
let inline isInfinity x = (^a : (static member IsInfinity : ^a -> bool) x)
let inline isFinite x = not (isNaN x) && not (isInfinity x)

SDAR 学習

次に SDAR 学習を実装しますが，その前にモデルのパラメーター推定の準備をします。といっても単純に連立方程式を解く関数を用意するだけです。ここでは Math.NET Numeric を使います。単純に LU 分解を利用するだけです。

open MathNet.Numerics.LinearAlgebra.Double

/// a * x = b を解きます。
let solve a b =
   let a = matrix a
   let b = vector b
   let lu = a.LU ()
   lu.Solve (b) |> Seq.toArray

次に SDAR の実装です。外から与えられる不変パラメーターは，前のパラメーター情報をどの程度残して新しいパラメーターを構築するかを決める忘却パラメーターと， AR モデルの次数のみです。他のパラメーターは内部で更新していきます。

SDAR のスコア計算は 2 通り提案されていますが[B]，単純な対数損失 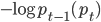，すなわち，新しいデータにおける直前までに得られたモデルへの適合度 (対数尤度) の符号を反転させたものを実装します。

type Sdar (discounting, order) =
   let mutable mu = nan
   let mutable sigma = nan
   let window = order + 1
   let c = Array.zeroCreate<float> window
   let w = Array.zeroCreate<float> order
   let r = discounting
   let series = Series (window)
   let s = 1.0 - r
   let interpolate a b = s * a + r * b

   let predict () = mu + Array.sum (Array.mapi (fun i w -> w * (series.GetBack (i + 1) - mu)) w)

   let score () =
      let xt = series.GetBack (0)
      let s = predict ()
      let residual = xt - s
      let v = 2.0 * sigma
      0.5 * float window * log (v * Math.PI) + residual * residual / v

   member __.Update (x) =
      series.Append (x)
      if isNaN x then
         nan
      else
         mu <- if isNaN mu then series.Mean else interpolate mu x
         for j = 0 to order do
            let y = series.GetBack (j)
            if not (isNaN y) then
               let v = (x - mu) * (y - mu)
               c.[j] <- interpolate c.[j] v
         let a = [for j in 1 .. order -> [for i in 1 .. order -> c.[abs (j - i)]]]
         let b = [for j in 1 .. order -> c.[j]]
         Array.blit (solve a b) 0 w 0 order
         let xt = predict ()
         sigma <- if isNaN sigma then series.Var else let y = x - xt in interpolate sigma (y * y)
         score ()

Update を呼ぶと，スコアが返ってくるようになっています[C]。ちなみに時系列オブジェクトにデータを追加した後に NaN かどうかのチェックを行っていますが， NaN のまま計算をすすめていっても問題なく動くはずです。

ChangeFinder

さていよいよ ChangeFinder アルゴリズムの実装です。といっても SDAR 学習を 2 段階で繰り返すのとスコアの平滑化を行うだけなので，とても単純です。

type Learning = {
   Model : Sdar
   Scores : Series
}

type ChangeFinder (discounting, order, smoothing) =
   let first = { Model = Sdar (discounting, order); Scores = Series (smoothing) }
   let second = { Model = Sdar (discounting, order); Scores = Series (smoothing) }

   let update (learn:Learning) x =
      x |> learn.Model.Update |> learn.Scores.Append
      learn.Scores.Mean

   member __.Next (x) =
      x |> update first |> update second

第 1 学習に対して Update を呼ぶとスコアが返されるのでそれをスコア系列に保存します。スコア系列を平滑化したものが第 2 系列になるので，同じ処理を第 2 学習に与えて結果を最終スコアとして得ます。なのでこの処理を update という関数に切り出せば，パイプで 2 回それぞれの学習器に対して繰り返すだけです。

ちなみに上記実装ではオリジナル時系列の第 1 学習と対数損失の第 2 学習でパラメーター (忘却パラメーター， AR モデルの次数，平滑化ウィンドウ幅) を同じ値にしていますが，これは単純化のためで，別の値を与えることは問題ないはずです。

使ってみる

使い方は簡単です。オブジェクトを作ってアップデートしていくだけです。サンプルデータは，参考文献にある Python で実装されている ChangeFinder の例を使用しています。

open FsRandom
open FsRandom.Statistics

let data =
   let state = createState xorshift (123456789u, 362436069u, 521288629u, 88675123u)
   let generators =
      Random.mergeWith Array.concat <| [
         Array.randomCreate 300 <| normal (0.7, 0.05)
         Array.randomCreate 300 <| normal (1.5, 0.05)
         Array.randomCreate 300 <| normal (0.6, 0.05)
         Array.randomCreate 300 <| normal (1.3, 0.05)
      ]
   Random.get generators state

このデータに対して以下のように ChangeFinder を使います。

let finder = ChangeFinder (0.01, 1, 7)
Seq.map finder.Next data

結果をプロットすると，以下のようになります。軸がずれて見づらいですが，変化した場所に対してスコアが上がっているので，きちんと変化点を検出できています。

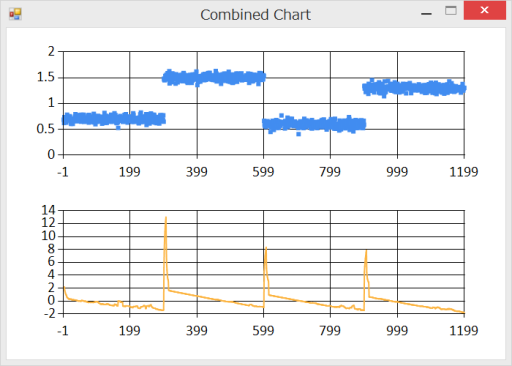
changefinder

しかしこの例ではうまく動いていますが，参考文献にも書かれている通りパラメーターのチューニングが実際のデータに対しては重要になってきます。あと多次元化ですね。もともと ChangeFinder は多次元に対応した手法ですので。

参考文献

更新履歴

  • [2014-05-13 19:30 更新] スコア計算時のモデル予測の係数が誤っていたのを修正[D]。

脚注

  1. 本当は無限大は発散してしまったケースでしょうから，別途考えるべきですね。 [↩]
  2. もう一方のスコアについては参考文献を参照してください。 [↩]
  3. 単にデータを加えて行ってパラメーターを更新するだけという作業があるなら，毎回スコアを計算するのは無駄ですね。 [↩]
  4. 対数損失なのに桁が大きい時点で間違っていると気付くべきでした。 [↩]

© Copyright 2014 - 捨てられたブログ

Colorbox Theme byTheme Mansion, Proudly Powred by WordPress