多変量正規分布にしたがう乱数の生成

多変量正規分布にしたがう乱数を生成したい場合のお話です。正規分布は条件付き確率も正規分布なので Gibbs サンプラーを容易に構築できるのですが，互いに独立な乱数が生成できるのであればそれにこしたことはありません。ということで互いに独立な多変量正規乱数を生成できるようにします。

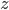を各次元の要素が独立に標準単変量正規分布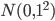にしたがう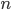次元の乱数ベクトルであるとします。言い換えれば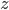は多変量正規分布 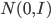( 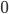は零ベクトル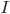，は単位行列) にしたがっています。これから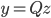となる変換をほどこしたときに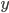が目的分布 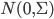( 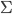は共分散行列) にしたがうように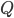を定めます。そうすれば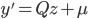は明らかに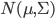にしたがいます。

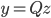による変換により，次のようにして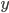の平均が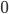で共分散行列が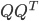となることがわかります。

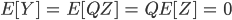
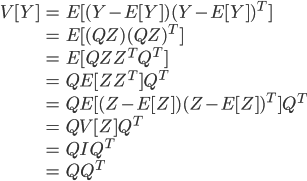
したがって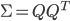となるように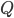を定めれば良いことになります。ここで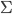は実対称行列なので対角化可能で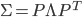となるような直行行列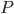および固有値を対角成分に持つ行列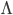が存在します。さらに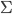は共分散行列なので，半正定値行列です。つまり固有値はすべて 0 以上の実数です。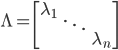とすれば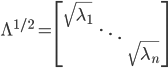とすることができます。そして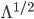は対角行列なので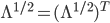となります。したがって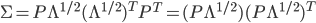となり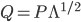，とすれば良いことがわかります。

さて実際にこのような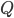を構築するのには，たとえばヤコビ法やコレスキー分解を用います。いずれも適用できる条件がありますが，共分散行列はいずれの条件も満たしています。ここでは気分的にヤコビ法を採用します^{[ とする時点でコレスキー分解で良いのですが，最初その発想にいたらなくて対称行列からヤコビ法しか知らなかったのでこれを選んだというのは内緒。">A]}。

let sqrtsumsq x y =
   if abs x > abs y then
      let r = y / x
      in abs x * sqrt (1.0 + r * r)
   elif y <> 0.0 then
      let r = x / y
      in abs y * sqrt (1.0 + r * r)
   else
      0.0

let diag n = Array2D.init n n (fun i j -> if i = j then 1.0 else 0.0)

let epsilon = pown 2.0 (-52)
let jacobi matrix =
   let n = Array2D.length1 matrix
   let m = n - 1
   let eigenvalues = Array2D.copy matrix
   let eigenvectors = diag n
   let findMax () =
      seq {
         for i = 0 to m do
            for j = 0 to m do
               if i <> j then
                  yield (i, j), abs eigenvalues.[i, j]
      }
      |> Seq.maxBy snd
   let loop = ref true
   while !loop do
      let (p, q), max = findMax ()
      if max < epsilon then
         loop := false
      else
         let app = eigenvalues.[p, p]
         let aqq = eigenvalues.[q, q]
         let apq = eigenvalues.[p, q]
         let t = 0.5 * (app - aqq)
         let ss = 0.5 * (1.0 - abs t / sqrtsumsq apq t)  // sin^2
         let cc = 1.0 - ss  // cos^2
         let s = if apq * t > 0.0 then -sqrt ss else sqrt ss  // sin
         let c = sqrt cc  // cos
         let sc = s * c  // sin * cos
         for i = 0 to m do
            let api = eigenvalues.[p, i]
            let aqi = eigenvalues.[q, i]
            eigenvalues.[p, i] <- api * c - aqi * s
            eigenvalues.[q, i] <- api * s + aqi * c
         for i = 0 to m do
            eigenvalues.[i, p] <- eigenvalues.[p, i]
            eigenvalues.[i, q] <- eigenvalues.[q, i]
         eigenvalues.[p, p] <- app * cc - 2.0 * apq * sc + aqq * ss
         eigenvalues.[q, q] <- aqq * cc + 2.0 * apq * sc + app * ss
         eigenvalues.[p, q] <- 0.0
         eigenvalues.[q, p] <- 0.0
         for i = 0 to m do
            let aip = eigenvectors.[i, p]
            let aiq = eigenvectors.[i, q]
            eigenvectors.[i, p] <- aip * c - aiq * s
            eigenvectors.[i, q] <- aip * s + aiq * c
   eigenvalues, eigenvectors

事前に必要となる標準正規乱数の生成は，たとえば Box-Muller 変換を用います。

let random = System.Random ()
let rec boxMuller () = seq {
   let r = sqrt <| -2.0 * log (random.NextDouble ())
   let theta = 2.0 * System.Math.PI * (random.NextDouble ())
   yield r * cos theta
   yield r * sin theta
   yield! boxMuller ()
}

これらを用いて多変量正規分布にしたがう乱数を生成します。

let multiply a b =
   let m = Array2D.length1 a
   let k = Array2D.length2 a
   let n = Array2D.length2 b
   let p = Array2D.zeroCreate m n
   for i = 0 to m - 1 do
      for j = 0 to n - 1 do
         let mutable sum = 0.0
         for t = 0 to k - 1 do
            sum <- sum + a.[i, t] * b.[t, j]
         p.[i, j] <- sum
   p

let multiplyVector a x =
   let m = Array2D.length1 a
   let n = Array.length x
   let p = Array.zeroCreate m
   for i = 0 to m - 1 do
      let mutable sum = 0.0
      for t = 0 to n - 1 do
         sum <- sum +  a.[i, t] * x.[t]
      p.[i] <- sum
   p

let multinormal mu sigma =
   let n = Array.length mu
   let eigenvalues, eigenvectors = jacobi sigma
   let d = Array2D.map sqrt eigenvalues
   let q = multiply eigenvectors d
   let z = boxMuller () |> Seq.take n |> Seq.toArray
   Array.map2 (+) mu (multiplyVector q z)

ということでいつでも多変量正規分布にしたがう互いに独立な乱数が生成できるようになりました。

脚注

本当は正定値行列を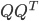とする時点でコレスキー分解で良いのですが，最初その発想にいたらなくて対称行列からヤコビ法しか知らなかったのでこれを選んだというのは内緒。 [↩]

捨てられたブログ

脚注