異常領域を含む時系列データの平滑化

以下のようなデータ列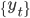を考えます。

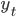は隠れ状態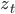に依存する乱数。
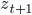は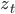から確率的に決まる。

具体的に，以下のようなのデータ列を考えます。

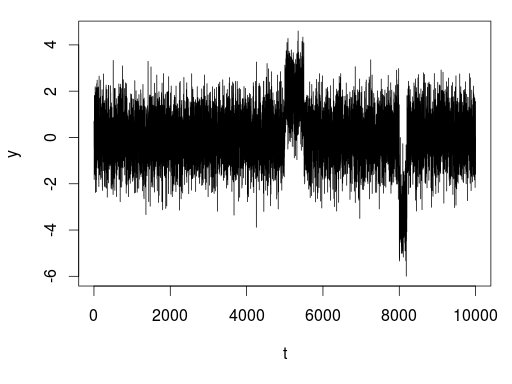
state

t が 5,000 から 5,500 までの領域と 8,000 から 8,200 までの領域が通常と異なる振る舞いを起こしていることが見て取れます (そのように生成したものです)。

こういったデータから異常領域を推定するのは隠れマルコフモデルが有効ですが^[A]，ここではより単純に，平滑化によって異常領域を視覚化する方法を紹介します。元ネタは Rippe et al. (2012) です。

この手法は，平滑化したデータ列と実際のデータ列の差と，平滑化したデータ列内での変化にそれぞれペナルティを課し，そのペナルティを最小化するという手法です。 Whittaker (1923) の平滑化スプラインを少し改変したものになります。詳細は論文を読んでいただくとして，それを R で実装してみたのが以下です。

segmented.smooth <- function(x, lambda, beta, q=0, iteration=5L) {
   require(spam)
   n <- length(x)
   I <- diag.spam(1, n)
   D <- diff(I)
   tD <- t(D)
   x <- as.spam(x)
   z <- solve(I + lambda * tD %*% D, x)
   if (beta == 0) {
      iteration <- 0L
   } else {
      b2 <- rep(beta ^ 2, n - 1)
   }
   e <- (q - 2) / 2
   while (iteration > 0L) {
      Dz <- as.numeric(D %*% z)
      v <- Dz ^ 2 + b2
      V <- diag.spam(v ^ e)
      z <- solve(I + lambda * tD %*% V %*% D, x)
      iteration <- iteration - 1L
   }
   z
}

spam パッケージは論文中でも言及されている通り疎行列を扱うためのパッケージです。

前述のデータは以下のような感じに平滑化されます。ここでは lambda = 10， beta = 0.001 としました。

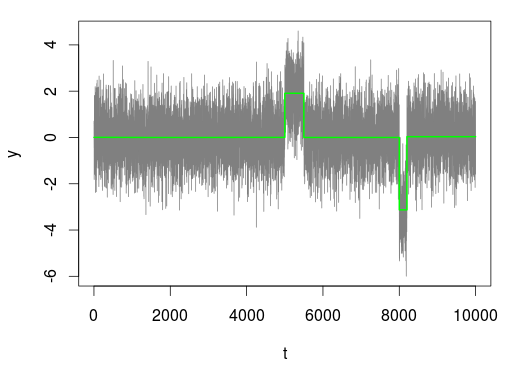
smooth

lambda が大きいと多少の異常領域は無視され，小さいと過敏に反応します。 beta が大きいときれいに平滑化されません。いまいちパラメーターと抽出される領域の範囲との関係が明瞭ではありませんが，パラメーターをうまく決められれば非常に見やすい結果が得られます。

脚注

たとえば『Anomaly Detection with Hidden Markov Model(HMM)』を参照。 [↩]

捨てられたブログ

脚注