微分は積分に比べて解析的に求まるケースが多いのであまり使われる場面は少ないですが，それでも数値計算的に微分係数が求められると嬉しいです。簡易的に適当に小さい 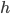を持ってきて 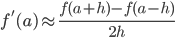で計算することができるのですが，精度が良くありません。

もともと上の計算方法はテイラー展開，

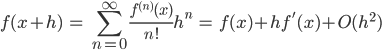
および

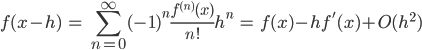
の差をとって 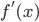について整理したものです。

ここで更に 2 次展開した場合を考えます。すなわち

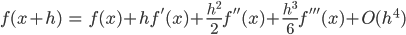
と

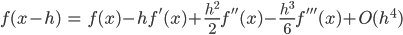
の差をとって

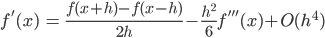
を得ます。このままでは 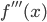があって計算できないので，これを消すことを考えます。

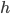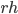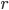上式 (1 式とします) の を ( は任意の定数) で置き換えると，直ちに

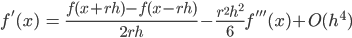
を得ます (2 式とします)。 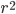× (1 式) - (2 式) によって 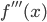を消す事ができ，次の近似式を得ます。

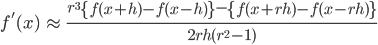
このような操作を繰り返すと更に精度を上げることも可能です。

なお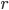， の値として 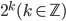を用いるのが良いみたいです。