Nemerle のステートチャートマクロ

新しいビルドには Nemerle.Statechart というライブラリーが同梱されています。これは UML のステートチャート図 (に相当する DSL) からその状態遷移を表すクラス群を自動生成するためのマクロです。

例えば次のようなお天気モデルを考えてみましょう。まず初日の天気は晴れであるとします。翌日以降の天気は，前の日の天気から一定の確率により決まるとします。前日が晴れの場合，次の日も晴れである確率は 0.8，雨である確率は 0.2 とし，前日が雨の場合，次の日が晴れである確率と雨である確率は各々 0.5 とします (下図参照)。

前日が晴れのとき，翌日が晴れである確率は 0.8，雨である確率は 0.2，前日が雨のときは翌日が晴れである確率と雨である確率は各々 0.5

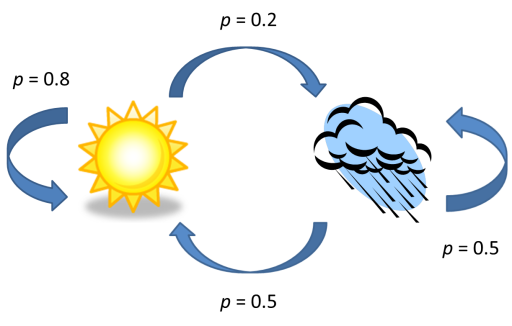
これを Nemerle.Statechart を使って次のように表すことができます。

using Nemerle.Statechart;

[statechart(<#
   flags : auto_initial;
      
   state Weather
   {
      0 => Sunny;
         
      state Sunny
      {
         NextDay [SunnyToRainy] => Rainy;
         else => @;
      }
         
      state Rainy
      {
         NextDay [RainyToSunny] => Sunny;
         else => @;
      }
   }
#>)]
public class WeatherFsm
{
}

これを Nemerle.Statechart.dll を参照してコンパイルすれば OK です^[A]。クラス名のサフィックス Fsm は有限ステートマシン (finite state machine) のことです。

コード中の 0 は初期状態を， @ は自分自身の状態を表します。また， [] は条件です。つまり上のコードは，「 Weather という状態はまず最初に Sunny 状態に遷移する。 Sunny 状態では NextDay というアクションを起こして SunnyToRainy であれば Rainy 状態に移行し，そうでなければ現在の状態にとどまる。 Rainy 状態では NextDay というアクションを起こして RainyToSunny であれば Rainy 状態に移行し，そうでなければ現在の状態にとどまる」という状態遷移を表します。

このクラスにはどの状態からどの状態へ遷移するかという情報は含まれていますが，その遷移確率に関する情報は記述されていません^[B]。定義した状態遷移を利用して上記のお天気モデルを作成します。

using System;
using Nemerle.Extensions;

public class WeatherModel
{
   private random : Random;
   private fsm : WeatherFsm;
   private mutable p : double;
   
   public this()
   {
      this.random = Random();
      this.fsm = WeatherFsm() <- {
         GuardNodeSunnyToRainy = SunnyToRainy;
         GuardNodeRainyToSunny = RainyToSunny;
      };
      this.fsm.Initiate();
   }
   
   private SunnyToRainy() : bool
   {
      this.p < 0.2;
   }
   
   private RainyToSunny() : bool
   {
      this.p < 0.5;
   }

   private UpdateRandom() : void
   {
      this.p = this.random.NextDouble();
   }
   
   public MoveNext() : bool
   {
      UpdateRandom();
      this.fsm.NextDay();
      !this.fsm.IsTerminated;
   }
   
   public Current : WeatherFsm.State
   {
      get { this.fsm.CurState; }
   }
}

このクラスはメンバーとして乱数生成器 (random) と現在の乱数 (p) と，先ほど作成した状態遷移クラスを持っています。 14, 15 行目で GuardNode... という名前のプロパティにそれぞれの天気の推移確率の条件を返す関数与えています。コンパイル時に状態遷移の際に定義した条件名が GuardNode... の ... になっていることがわかります。そして MoveNext では乱数の状態を更新して状態遷移を行います^[C]。

使い方は単純です。

using System.Linq;
using Nemerle.Collections;

using System.Console;

def chainLength = 10000;
def burnin = 2000;
def sampleCount = chainLength - burnin;
def model = WeatherModel();
Enumerable.Range(0, chainLength)
          .Select(fun (_)
          {
             _ = model.MoveNext();
             model.Current;
          })
          .Skip(burnin)
          .GroupBy(weather => weather)
          .Iter(fun (g : IGrouping[WeatherFsm.State, WeatherFsm.State])
          {
             def weather = g.Key;
             def weatherCount = g.Count();
             WriteLine("{0} = {1} ({2:P})", weather, weatherCount, (weatherCount : double) / sampleCount);
          });

10,000 日分の天気を取得し，先頭の 2,000 日を除いた 8,000 日分のデータについて晴れと雨の日数を集計して出力します。実行すると晴れが 7 割強になります^[D]。

まとめ

Nemerle.Statechart を使うと状態遷移が起こるプログラムが容易に書けます。ここでは非常に単純な例を持ち出しましたが，より複雑なケースにも対応しています^[E]。詳細なドキュメントは https://github.com/CodingUnit/Nemerle.Statechart/wiki にありますが，ロシア語なので私には読めません。 Nemerle には非常に興味深いライブラリーがたくさんありますね。ドキュメントが少ないのが玉に瑕ですが。

脚注

Nemerle.Statechart.dll はマクロライブラリーなので，コンパイルした後は参照不要です。 [↩]
クラス内部に記述することもできますが，外部で記述した方が柔軟になります。クラス内に定義する場合は同名のプロパティを定義するかマクロを利用します。 [↩]
おそらくここは正しくなくて，本当なら状態遷移のタイミングで乱数更新アクションを定義して呼ぶのでしょうが，以下のようにやってみても期待したように動いてくれませんでした。どうやら同じ状態に遷移する (=> @) 際にはアクションが起こらないようです。ステートチャートに詳しくないのでこれが正しい挙動なのかどうかはわかりかねます。
```
state Sunny
{
   $> / Update;
   NextDay [SunnyToRainy] => Rainy;
   else => @
}

WeatherFsm() <- {
   UpdateAction += UpdateRandom;
}
```
[↩]
理論的には試行回数を増やせば 5/7 に収束します。興味がある方は teramonagi 氏の『マルコフ連鎖モンテカルロ法入門-１』をご参照ください。数値は違いますが内容は同じことをやっています。 [↩]
例えばテストではファイルの編集状態を扱っています。 [↩]

捨てられたブログ

まとめ

脚注