無理数 FizzBuzz を Nemerle で解いてみたという話。無理数 FizzBuzz は以下のような問題です。

無理数 FizzBuzz

自然数を列挙しながら、円周率の整数倍の整数部に等しいときは“Fizz”と言い、自然対数の底の整数倍の整数部に等しいときは“Buzz”と言い、両方であるときは“FizzBuzz”と言う遊び。

Nemerle は遅延評価が使えるので，整数と円周率の整数倍と自然対数の底の整数倍をキープしながら無限リストを作ったらいいんじゃないという方針です。

using Nemerle;
using Nemerle.Utility;

using System.Math;

public class FizzBuzzList
{
   private n : int;
   private pi : double;
   private e : double;
   [Accessor]
   private next : LazyValue[FizzBuzzList];

   public this()
   {
      this.n = 1;
      this.pi = PI;
      this.e = E;
      this.next = lazy(FizzBuzzList(2, PI, E));
   }

   private this(n : int, pi : double, e : double)
   {
      this.n = n;
      this.pi = pi;
      this.e = e;
      def nextN = n + 1;
      def nextPi = if (nextN > pi) pi + PI else pi;
      def nextE = if (nextN > e) e + E else e;
      this.next = lazy(FizzBuzzList(nextN, nextPi, nextE));
   }

   public override ToString() : string
   {
      match (n == Floor(pi), n == Floor(e))
      {
         | (true, true) => "FizzBuzz";
         | (true, false) => "Fizz";
         | (false, true) => "Buzz";
         | (false, false) => n.ToString();
      }
   }
}

mutable fizzbuzz = FizzBuzzList();
repeat (100)
{
   System.Console.WriteLine(fizzbuzz);
   fizzbuzz = fizzbuzz.Next;
}

結果がこちら。

1
Buzz
Fizz
4
Buzz
Fizz
7
Buzz
Fizz
Buzz
11
Fizz
Buzz
14
Fizz
Buzz
17
Fizz
Buzz
20
FizzBuzz
22
23
Buzz
Fizz
26
Buzz
Fizz
Buzz
30
Fizz
Buzz
33
Fizz
Buzz
36
Fizz
Buzz
39
FizzBuzz
41
42
FizzBuzz
44
45
Buzz
Fizz
Buzz
49
Fizz
Buzz
52
Fizz
Buzz
55
Fizz
Buzz
58
FizzBuzz
60
61
FizzBuzz
63
64
FizzBuzz
66
Buzz
68
Fizz
Buzz
71
Fizz
Buzz
74
Fizz
Buzz
77
FizzBuzz
79
80
FizzBuzz
82
83
FizzBuzz
85
Buzz
Fizz
88
Buzz
90
Fizz
Buzz
93
Fizz
Buzz
96
FizzBuzz
98
99
FizzBuzz

おまけ

遅延リストじゃなくて n 番目の数に対して O(1) で出力を求めたいという欲求が。

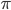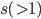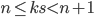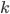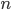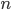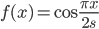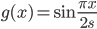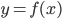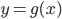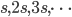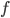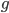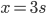や に相当する無理数を一般的に とします。このとき整数 となるような正の整数 が存在するような に対して Fizz や Buzz というような文字列を出力し，そうでなければ を出力するという処理を考えます。以下ではやや厳密な議論を避けてざっくりとした手法を説明します。 さて，なんとなく周期性を感じる場合は三角関数を使うというのが常套手段です。天下り的ですが， ， という 2 つの関数を考えます。 xy 平面上の 2 曲線 および のいずれかが x 軸と交差するのは のときです。 のとき ， のとき ， のとき 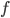，…というように 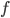と 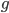が交互に x 軸と交差します。

そこで 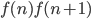という量を考えてみましょう。区間 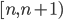において，曲線 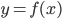は x 軸と高々 1 回しか交差しません。したがって，交差する場合は 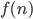と 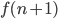の正負が逆転するので負に，交差しない場合は 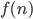と 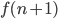の正負が一致するので正になります。 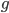についても同様のことが言えます。

さて，区間 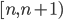において一方の曲線が x 軸と交差するとき，他方の曲線は x 軸と交差しうるでしょうか。答えはノーです。一方が交差するということは 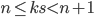となるような自然数 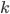が存在しているということです。今 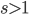を仮定しているので 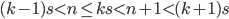です。一方が 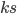で x 軸と交差するので，他方が x 軸と交差するのは 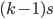と 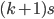です。したがって一方の曲線が x 軸と交わる場合，他方の曲線は x 軸と交わりません。 区間 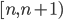において一方の曲線が x 軸と交差するならば，他方の曲線は x 軸と交差しないことがわかりました。ということは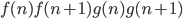， (これを 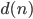とおきます) は負になります。また，区間 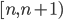において両方の曲線とも x 軸と交差しないなら 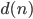は正です。逆に 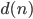が負なら一方の曲線が x 軸と交差し，正ならいずれも交差しません。 以上から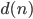， が FizzBuzz の判別に利用できることがわかります。すなわち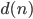， が正なら数字をそのまま出力し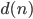， が負なら Fizz などの文字列を出力すればよさそうです。 以上を実装したのが次のコードです。 [code language="nemerle"] using Nemerle.Collections; using System.Math; def d(n, s) { def u = PI / s; def x = (2 * n + 1) * u; Cos(x) >= Cos(u); } def isFizz = d(_, PI); def isBuzz = d(_, E); def fizzbuzz(n) { match (isFizz(n), isBuzz(n)) { | (true, true) => "FizzBuzz"; | (true, false) => "Fizz"; | (false, true) => "Buzz"; | (false, false) => n.ToString(); } } $[1..100].Map(fizzbuzz).Iter(System.Console.WriteLine); [/code] 結果は先ほどと同様になります。 コード中では 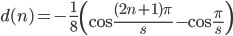と簡単な形に展開して，括弧の中身の正負を判別に利用しています。判別の不等号に = が付いているのは，上の議論では省略していましたが，区間の端がちょうど 0 になるときのためです (円周率も自然対数の底も無理数なので n が 0 のときのみ起こる)。

ソースコード

ソースコードは GitHub にて公開しています。