生態学の被食者・捕食者の個体数変動を,以下の方程式 (Lotka-Volterra 方程式) で表現するモデルがあります。
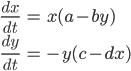
ここで 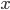 は被食者の個体数,
は被食者の個体数, 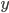 は捕食者の個体数を表します。
は捕食者の個体数を表します。
解析的に解くことが困難であるため,計算機によるシミュレーションを行うのが普通です。これを Haskell で実装してみました。
data Fractional t => Model t = Lv t t t t
data Fractional t => N t = N { prey :: t, predator :: t }
delta dt (Lv a b c d) (N { prey = x, predator = y }) =
N { prey = x * (a - b * y) * dt,
predator = -y * (c - d * x) * dt }
move n dn = N { prey = prey n + prey dn,
predator = predator n + predator dn }
mean d1 d2 = N { prey = (prey d1 + prey d2) / 2,
predator = (predator d1 + predator d2) / 2 }
next dt param (t, n) = let d1 = delta dt param n
d2 = delta dt param $ move n d1
in (t + dt, move n $ mean d1 d2)
lv dt param n0 = iterate (next dt param) (0, n0)
パラメーターを 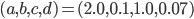 ,初期値を
,初期値を 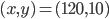 として,
として,  を 0.02 刻みで 1,200 回計算してみました[A]。
を 0.02 刻みで 1,200 回計算してみました[A]。
take 1200 $ lv 0.02 (Lv 2.0 0.1 1.0 0.07) (N { prey = 120, predator = 10 })
上記の関数そのままでは出力できませんが,適当に CSV で出力して R でグラフ化したのが以下の図です。
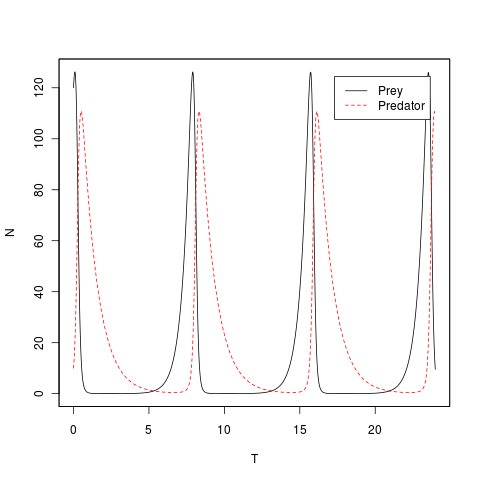
きれいに周期的に変動していますね。
脚注
- 選んだパラメーターや計算回数に特に意味はありません。 [↩]
