モンテカルロ法は乱数を用いる数値計算手法です。 F# の練習のためにモンテカルロ法を F# で実装してみました。計算するのはおなじみの円周率ですが,よく見かけるモンテカルロ積分[A]ではなく,棄却サンプリング法によりレイリー分布にしたがう乱数を取得し,その期待値を用いて円周率を計算してみました。
実装
open System
open System.Collections.Concurrent
[<AbstractClass>]
type MonteCarloMethod<'TParameter> () =
abstract Initialize: unit -> unit
default this.Initialize () = ()
abstract NextCandidate: unit -> 'TParameter
abstract Accept: 'TParameter -> bool
member this.Sample () =
this.Initialize ()
let collection = new BlockingCollection<'TParameter> ()
let sampleAsync = async {
while not collection.IsAddingCompleted do
this.SampleOne collection
}
Async.Start sampleAsync
collection.GetConsumingEnumerable()
member private this.SampleOne collection =
while not collection.IsAddingCompleted do
let candidate = this.NextCandidate ()
lock collection (fun () ->
if this.Accept candidate && not collection.IsAddingCompleted
then
collection.Add candidate
)
let rayleigh =
let f x = x * exp (x - x * x / 2.0)
let sup = let x = (1.0 + sqrt 5.0) / 2.0 in f x
let random = new Random ()
in
{
new MonteCarloMethod<double> () with
override this.NextCandidate () = let u = random.NextDouble () in -log u
override this.Accept x = sup * random.NextDouble () <= f x
}
rayleigh.Sample () |> Seq.take 10000 |> Seq.average |> fun x -> 2.0 * x * x |> printfn "%f"
F# の勉強をかねて書いてみたので,いろいろと F# の仕様を使っています。
MonteCarloMethod クラスは多相な抽象クラスです。 C# だと継承クラスを書く必要がありますが,ここではオブジェクト式を使って匿名型のインスタンスを作成しています。例のコードでは Initialize は特に何もしていませんね。
SampleOne メソッドはコレクションにサンプルを格納するためのメソッドで,並列化のために unit 型を返すようにしています。 Sample は外部から呼ぶためのメソッドで,内部的には SampleOne を async で呼んでいます[B]。
理論
棄却サンプリング法により,分散 1 のレイリー分布からの乱数をサンプリングしています。期待値は 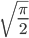 なので, 10000 個の乱数を取得し,その平均を二乗して 2 倍した結果を円周率として出力しています。
なので, 10000 個の乱数を取得し,その平均を二乗して 2 倍した結果を円周率として出力しています。
棄却サンプリングは目的分布 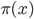 からのサンプリングが難しい際に,サンプリングが容易な分布
からのサンプリングが難しい際に,サンプリングが容易な分布 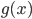 を利用します。ある定数
を利用します。ある定数  が存在して,すべての
が存在して,すべての 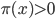 なる
なる 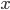 に対して
に対して 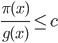 ならば,
ならば,  と
と 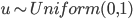 (一様乱数) を発生させ,
(一様乱数) を発生させ, 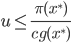 ならば
ならば 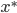 を採択するという手順を繰り返すにより,
を採択するという手順を繰り返すにより, 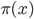 からの乱数が取得できます。分散 1 のレイリー分布の確率密度関数 (
からの乱数が取得できます。分散 1 のレイリー分布の確率密度関数 (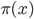 ) は
) は 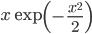 で,ここでは
で,ここでは 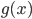 として母数 1 の指数分布の確率密度関数
として母数 1 の指数分布の確率密度関数 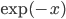 を選択しています。確率密度関数の比を取って微分すれば,
を選択しています。確率密度関数の比を取って微分すれば, 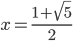 で最大値をとることが容易にわかるので,そのときの比の値を
で最大値をとることが容易にわかるので,そのときの比の値を  としています。
としています。
指数分布にしたがう乱数の生成は容易で,単に一様乱数の自然対数を取ってマイナスをとるだけです[C]。
参考文献
更新履歴
- [2011-06-23 23:35+0900] 比の上限が定数 c じゃなくて 1 になっていたのを修正。
- [2011-07-01 02:50+0900] 非同期の手法およびレイリー分布にしたがう乱数を直接取得する方法について追記。
脚注
- 1 辺の長さが 2 の正方形に無作為な点を落とし,それが正方形に内接する半径 1 の円に含まれるかどうかを判定し,円の中に落ちた点の割合から円周率を求める方法。 [↩]
- ここでは開始した非同期処理を終了させる方法について提供していません。生成した乱数を処理してすぐにプログラムが終了するので…という言い訳をしておきます。 [↩]
- 実はレイリー分布にしたがう乱数の生成も簡単で,期待値 2 の指数分布にしたがう乱数の平方根をとる,つまり一様乱数 u に対して √(-2 log u) をとれば良いです。ちなみにこの方法はボックス・ミューラーの方法で正規分布にしたがう乱数を生成するのに利用されています。 [↩]
