この記事は「R Advent Calendar 2015」の 23 日目の記事です。
アドベントカレンダーも終盤ですね。 アドベントというのはもともとクリスマスまでの期間を楽しむイベントとのことです。
クリスマスといえばイエス・キリストの誕生日です。そして今日は日本では天皇誕生日ということで，天皇の誕生日です。というわけで唐突に以下のような疑問が浮かびます。
- アドベントカレンダーに参加した人々に同じ誕生日の人はいる確率はどのくらいだろうか。
- 自分の誕生日に記事を書くイベントを開催した場合，何人くらい集まれば 1 年間のすべての日付を網羅できるだろうか。
雑な前振りですが，クリスマスで浮かれているのでこれでなんとかなると信じて先に進みます。
前提
さて，最初から残念なお知らせがあります。このタイプの問題を解く際には，だいたい以下のような前提をおかなければなりません。
- どの日付に人が生まれるかは同様に確からしい
- 2 月 29 日の存在は無視する
1 つ目は単純な確率として計算するための仮定ですね。実際は誕生日はばらつきがあるのですが，計算の都合上無視します。 2 つ目は無視してもしなくても良いのですが，同様に確からしいとした時に 4 年に 1 度しかこない日付ってどうなのっていう面倒な問題を無視するための仮定です。
Birthday Problem
最初の問題は Birthday Problem という名前で知られる問題です。よく「クラスの中に同じ誕生日の学生がいる確率」という言い方をしますが，今回はアドベントカレンダーの参加者としてみました。
同じ人がいる確率を直接計算するのは難しいので，全員の誕生日が異なる確率を 1 から引くことでその確率を得ます。 R Advent Calendar には重複を除いて 24 人の参加者がいます。全員に順番に誕生日を宣言していってもらいます。最初の uri さんは，どの誕生日であっても最初なので他の人と誕生日が重複することはありません。次の kaneshin さんは， uri さんの誕生日を除いた 364 日のいずれかであれば誕生日は他の人と重複しません。なので 365 日中 364 日から選ばれれば，重複しないことになります。確率で言えば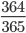 
です。同様に 3 番目の sinhrks さんは uri さんの誕生日と kaneshin さんの誕生日と異なる日付を選ぶので 
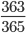です。一般に 
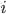番目の人の誕生日がそれまでの人と重複しない確率は 
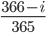です。
24 人の全員の誕生日が重複しない確率は，これらの積を計算すれば良いので，以下のようになります。
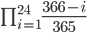
欲しい確率は同じ人がいる確率なので， 1 から引いて以下のような確率を得ます。
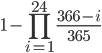
で，これが結局いくらなの，というのを R で計算します。
1 - prod((366 - 1:24) / 365)
[1] 0.5383443
5 割以上の確率で，アドベントカレンダー内に同じ誕生日の人がいるということですね。ちなみに私の誕生日は 2 月 25 日なので，何かください。
上記では直接計算しましたが， pbirthday 関数を利用するともっと簡単に計算できます。
pbirthday(24)
[1] 0.5383443
pbirthday 関数は， 3 人以上が同じ誕生日になる確率や，日付ではないサンプル空間を選ぶこともできます。これを使えばグループ内に 47 都道府県の同じ出身地の人がいる確率みたいなものも計算できますね。明らかに出身地は同様に確からしくないので正しい結果は得られませんが，話のネタくらいにはなるでしょう。ちなみにアドベントカレンダーの参加者中に 3 人以上同じ出身地の人がいる確率を求めると，以下のようになります。
pbirthday(24, classes = 47, coincident = 3)
[1] 0.5120386
出身地都道府県別にグループを作れば， 3 人以上のグループができる確率は 5 割以上ということですね。繰り返しますが，出身地の確率は等しくないので，この値は正確ではありません。
Coupon Collector's Problem
後者の問題は Coupon Collector's Problem という問題です。
先ほどと同様に考えます。 1 つ目の誕生日は誰が参加しても確率 1 で新しい誕生日です。 2 つ目の誕生日は確率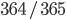 
で新しい誕生日になります。以下同様に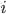， 日目の誕生日は 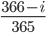の確率で新しい誕生日として集められます。まとめると， 1 人新しい人を連れて来た時，確率 
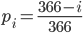で新しい誕生日となるわけです。
今求めたいのは，誕生日 365 日を網羅するために必要な人数の期待値です。 1 人新しい人を連れて来るというベルヌーイ施行を繰り返し，初めて新しい誕生日の人を連れてくるまでに必要な回数が欲しいので，ここでは幾何分布が利用できます。パラメーター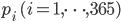 
の独立した幾何分布 
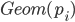の期待値の合計が求めたい期待値になります。
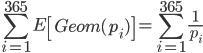
これを R で求めてみます。
p_i <- (366 - 1:365) / 365 sum(1 / p_i)
[1] 2364.646
2365 人いれば，すべての誕生日を網羅できることが期待されます。アドベントカレンダーを 100 個くらい集めて参加者を合わせれば網羅できそうですね。
ちなみに分散は同様に以下のようになります。
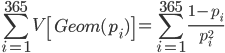
R で標準偏差を求めると以下のようになります。
sqrt(sum((1 - p_i) / p_i^2))
[1] 465.2066
ところでこの数を唐突に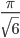 
で割ってみましょう。
sqrt(sum((1 - p_i) / p_i^2)) / (pi / sqrt(6))
[1] 362.7201
はい， 365 に近い値が出てきましたね。事象の数 
(ここでは誕生日の数 = 365) が大きい時は分散は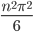 
で近似できます。同様に期待値は 
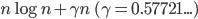で近似できます。 
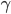はオイラーの定数というやつです。
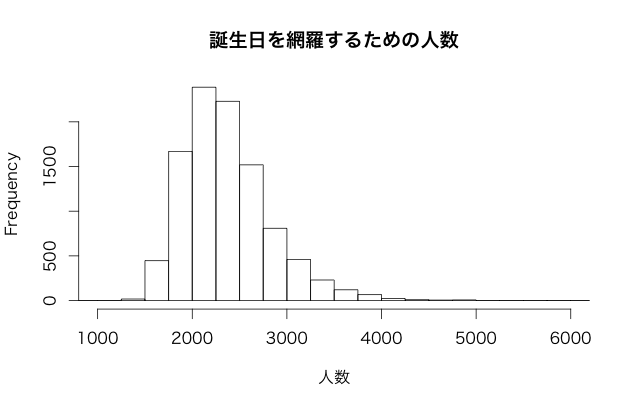
最後にシミュレーションしてどんな分布になるか確認してみましょう。
先ほど幾何分布は成功までの施行回数と言いましたが，幾何分布にはバリエーションがあって，成功までに失敗した回数というものもあります。両方の幾何分布は，分布の位置が 1 だけずれています。 R の幾何分布は後者を指すので，シミュレーションの際は rgeom 関数の結果に 1 を足すことを忘れないようにします。
rbirth <- function(n, classes) {
r <- function(., k) {
p_i <- seq(classes, 0) / classes
sum(rgeom(classes, p_i) + 1)
}
sapply(seq_len(n), r, k = classes)
}
hist(rbirth(10000, 365))
まとめ
誕生日ネタ 2 本でお送りしました。